Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T15:11:16.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Plasmoid instability in the semi-collisional regime

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  19 November 2018

Pallavi Bhat  and
Nuno F. Loureiro
Pallavi Bhat*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Nuno F. Loureiro
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: pbhat@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate analytically and numerically the semi-collisional regime of the plasmoid instability, defined by the inequality 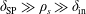$\unicode[STIX]{x1D6FF}_{\text{SP}}\gg \unicode[STIX]{x1D70C}_{s}\gg \unicode[STIX]{x1D6FF}_{\text{in}}$, where 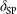$\unicode[STIX]{x1D6FF}_{\text{SP}}$ is the width of a Sweet–Parker current sheet, 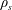$\unicode[STIX]{x1D70C}_{s}$ is the ion sound Larmor radius and 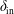$\unicode[STIX]{x1D6FF}_{\text{in}}$ is the width of the boundary layer that arises in the plasmoid instability analysis. Theoretically, this regime is predicted to exist if the Lundquist number 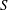$S$ and the length of the current sheet 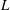$L$ are such that 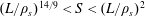$(L/\unicode[STIX]{x1D70C}_{s})^{14/9}<S<(L/\unicode[STIX]{x1D70C}_{s})^{2}$ (for a sinusoidal-like magnetic configuration; for a Harris-type sheet the lower bound is replaced with 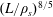$(L/\unicode[STIX]{x1D70C}_{s})^{8/5}$). These bounds are validated numerically by means of simulations using a reduced gyrokinetic model (Zocco & Schekochihin, Phys. Plasmas, vol. 18 (10), 2011, 102309) conducted with the code Viriato. Importantly, this regime is conjectured to allow for plasmoid formation at relatively low, experimentally accessible, values of the Lundquist number. Our simulations obtain plasmoid instability at values of 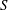$S$ as low as 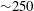${\sim}250$. The simulations do not prescribe a Sweet–Parker sheet; rather, one is formed self-consistently during the nonlinear evolution of the initial tearing mode configuration. This proves that this regime of the plasmoid instability is realizable, at least at the relatively low values of the Lundquist number that are accessible to current dedicated experiments.

Keywords

astrophysical plasmasplasma instabilitiesplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 6 , December 2018 , 905840607
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baalrud, S. D., Bhattacharjee, A., Huang, Y.-M. & Germaschewski, K. 2011 Hall magnetohydrodynamic reconnection in the plasmoid unstable regime. Phys. Plasmas 18 (9), 092108.Google Scholar
Baty, H. 2014 Effect of plasma- $\unicode[STIX]{x1D6FD}$ on the onset of plasmoid instability in Sweet–Parker current sheets. J. Plasma Phys. 80, 655–665.Google Scholar
Bhattacharjee, A., Huang, Y.-M., Yang, H. & Rogers, B. 2009 Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16 (11), 112102.Google Scholar
Biskamp, D. 1986 Magnetic reconnection via current sheets. Phys. Fluids 29, 1520–1531.Google Scholar
Biskamp, D. 2000 Magnetic Reconnection in Plasmas. Cambridge University Press.Google Scholar
Burch, J. L., Torbert, R. B., Phan, T. D., Chen, L.-J., Moore, T. E., Ergun, R. E., Eastwood, J. P., Gershman, D. J., Cassak, P. A., Argall, M. R. et al. 2016 Electron-scale measurements of magnetic reconnection in space. Science 352, aaf2939.Google Scholar
Cassak, P. A., Shay, M. A. & Drake, J. F. 2009 Scaling of Sweet–Parker reconnection with secondary islands. Phys. Plasmas 16 (12), 120702.Google Scholar
Cerri, S. S. & Califano, F. 2017 Reconnection and small-scale fields in 2D-3V hybrid-kinetic driven turbulence simulations. New J. Phys. 19 (2), 025007.Google Scholar
Cerutti, B., Uzdensky, D. A. & Begelman, M. C. 2012 Extreme particle acceleration in magnetic reconnection layers: application to the gamma-ray flares in the crab nebula. Astrophys. J. 746, 148.Google Scholar
Cerutti, B., Werner, G. R., Uzdensky, D. A. & Begelman, M. C. 2013 Simulations of particle acceleration beyond the classical synchrotron burnoff limit in magnetic reconnection: an explanation of the crab flares. Astrophys. J. 770, 147.Google Scholar
Comisso, L., Lingam, M., Huang, Y.-M. & Bhattacharjee, A. 2016 General theory of the plasmoid instability. Phys. Plasmas 23 (10), 100702.Google Scholar
Cowley, S. C., Kulsrud, R. M. & Hahm, T. S. 1986 Linear stability of tearing modes. Phys. Fluids 29, 3230–3244.Google Scholar
Daughton, W. & Roytershteyn, V. 2012 Emerging parameter space map of magnetic reconnection in collisional and kinetic regimes. Space Sci. Rev. 172, 271–282.Google Scholar
DiBraccio, G. A., Slavin, J. A., Imber, S. M., Gershman, D. J., Raines, J. M., Jackman, C. M., Boardsen, S. A., Anderson, B. J., Korth, H., Zurbuchen, T. H. et al. 2015 MESSENGER observations of flux ropes in Mercury’s magnetotail. Planet. Space Sci. 115, 77–89.Google Scholar
Dorfman, S., Ji, H., Yamada, M., Yoo, J., Lawrence, E., Myers, C. & Tharp, T. D. 2013 Three-dimensional, impulsive magnetic reconnection in a laboratory plasma. Geophys. Rev. Lett. 40, 233–238.Google Scholar
Drake, J. F. & Lee, Y. C. 1977 Kinetic theory of tearing instabilities. Phys. Fluids 20, 1341–1353.Google Scholar
Drake, J. F., Swisdak, M., Che, H. & Shay, M. A. 2006 Electron acceleration from contracting magnetic islands during reconnection. Nature 443, 553–556.Google Scholar
Dungey, J. W. 1961 Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47–48.Google Scholar
Forest, C. B., Flanagan, K., Brookhart, M. & Clark, M. 2015 The Wisconsin plasma astrophysics laboratory. J. Plasma Phys. 81, 345810501.Google Scholar
Fox, W., Bhattacharjee, A. & Germaschewski, K. 2012 Magnetic reconnection in high-energy-density laser-produced plasmasa). Phys. Plasmas 19 (5), 056309.Google Scholar
Frieman, E. A. & Chen, L. 1982 Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria. Phys. Fluids 25, 502–508.Google Scholar
Furth, H. P., Killeen, J. & Rosenbluth, M. N. 1963 Finite-resistivity instabilities of a sheet pinch. Phys. Fluids 6, 459–484.Google Scholar
Giannios, D., Uzdensky, D. A. & Begelman, M. C. 2009 Fast TeV variability in blazars: jets in a jet. Mon. Not. R. Astron. Soc. 395, L29–L33.Google Scholar
Guo, F., Liu, Y.-H., Daughton, W. & Li, H. 2015 Particle acceleration and plasma dynamics during magnetic reconnection in the magnetically dominated regime. Astrophys. J. 806, 167.Google Scholar
Hare, J. D.2017 High energy density magnetic reconnection experiments in colliding carbon plasma flows. PhD thesis, Imperial College London.Google Scholar
Hare, J. D., Lebedev, S. V., Suttle, L. G., Loureiro, N. F., Ciardi, A., Burdiak, G. C., Chittenden, J. P., Clayson, T., Eardley, S. J., Garcia, C. et al. 2017a Formation and structure of a current sheet in pulsed-power driven magnetic reconnection experiments. Phys. Plasmas 24 (10), 102703.Google Scholar
Hare, J. D., Suttle, L., Lebedev, S. V., Loureiro, N. F., Ciardi, A., Burdiak, G. C., Chittenden, J. P., Clayson, T., Garcia, C., Niasse, N. et al. 2017b Anomalous heating and plasmoid formation in a driven magnetic reconnection experiment. Phys. Rev. Lett. 118 (8), 085001.Google Scholar
Hare, J. D., Suttle, L. G., Lebedev, S. V., Loureiro, N. F., Ciardi, A., Chittenden, J. P., Clayson, T., Eardley, S. J., Garcia, C., Halliday, J. W. D. et al. 2018 An experimental platform for pulsed-power driven magnetic reconnection. Phys. Plasmas 25 (5), 055703.Google Scholar
Harris, E. G. 1962 On a plasma sheath separating regions of oppositely directed magnetic field. Il Nuovo Cimento 23, 115–121.Google Scholar
Hastie, R. J. 1997 Sawtooth instability in tokamak plasmas. Astrophys. Space Sci. 256, 177–204.Google Scholar
Howes, G. G., Cowley, S. C., Dorland, W., Hammett, G. W., Quataert, E. & Schekochihin, A. A. 2006 Astrophysical gyrokinetics: basic equations and linear theory. Astrophys. J. 651, 590–614.Google Scholar
Huang, Y.-M. & Bhattacharjee, A. 2010 Scaling laws of resistive magnetohydrodynamic reconnection in the high-Lundquist-number, plasmoid-unstable regime. Phys. Plasmas 17 (6), 062104.Google Scholar
Jackman, C. M., Slavin, J. A. & Cowley, S. W. H. 2011 Cassini observations of plasmoid structure and dynamics: implications for the role of magnetic reconnection in magnetospheric circulation at Saturn. J. Geophys. Res. Space Phys. 116, A10212.Google Scholar
Jara-Almonte, J., Ji, H., Yamada, M., Yoo, J. & Fox, W. 2016 Laboratory observation of resistive electron tearing in a two-fluid reconnecting current sheet. Phys. Rev. Lett. 117 (9), 095001.Google Scholar
Ji, H., Bhattacharjee, A., Prager, S., Daughton, W., Bale, S. D., Carter, T., Crocker, N., Drake, J., Egedal, J., Sarff, J. et al. 2015 FLARE (facility for laboratory reconnection experiments): a major next-step for laboratory studies of magnetic reconnection. In AAS/AGU Triennial Earth–Sun Summit, AAS/AGU Triennial Earth–Sun Summit, vol. 1, p. 104.05.Google Scholar
Ji, H. & Daughton, W. 2011 Phase diagram for magnetic reconnection in heliophysical, astrophysical, and laboratory plasmas. Phys. Plasmas 18 (11), 111207.Google Scholar
Kagan, D., Sironi, L., Cerutti, B. & Giannios, D. 2015 Relativistic magnetic reconnection in pair plasmas and its astrophysical applications. Space Sci. Rev. 191 (1), 545–573.Google Scholar
Lapenta, G. 2008 Self-feeding turbulent magnetic reconnection on macroscopic scales. Phys. Rev. Lett. 100 (23), 235001.Google Scholar
Lenard, A. & Bernstein, I. B. 1958 Plasma oscillations with diffusion in velocity space. Phys. Rev. 112, 1456–1459.Google Scholar
Liu, W., Chen, Q. & Petrosian, V. 2013 Plasmoid ejections and loop contractions in an eruptive M7.7 solar flare: evidence of particle acceleration and heating in magnetic reconnection outflows. Astrophys. J. 767, 168.Google Scholar
Loureiro, N. F. & Boldyrev, S. 2017 Role of magnetic reconnection in magnetohydrodynamic turbulence. Phys. Rev. Lett. 118 (24), 245101.Google Scholar
Loureiro, N. F., Cowley, S. C., Dorland, W. D., Haines, M. G. & Schekochihin, A. A. 2005 $X$ -point collapse and saturation in the nonlinear tearing mode reconnection. Phys. Rev. Lett. 95 (23), 235003.Google Scholar
Loureiro, N. F., Dorland, W., Fazendeiro, L., Kanekar, A., Mallet, A., Vilelas, M. S. & Zocco, A. 2016 Viriato: a Fourier–Hermite spectral code for strongly magnetized fluid-kinetic plasma dynamics. Comput. Phys. Commun. 206, 45–63.Google Scholar
Loureiro, N. F., Samtaney, R., Schekochihin, A. A. & Uzdensky, D. A. 2012 Magnetic reconnection and stochastic plasmoid chains in high-Lundquist-number plasmas. Phys. Plasmas 19 (4), 042303.Google Scholar
Loureiro, N. F., Schekochihin, A. A. & Cowley, S. C. 2007 Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14 (10), 100703.Google Scholar
Loureiro, N. F., Schekochihin, A. A. & Uzdensky, D. A. 2013 Plasmoid and Kelvin–Helmholtz instabilities in Sweet–Parker current sheets. Phys. Rev. E 87 (1), 013102.Google Scholar
Loureiro, N. F. & Uzdensky, D. A. 2016 Magnetic reconnection: from the Sweet–Parker model to stochastic plasmoid chains. Plasma Phys. Control. Fusion 58 (1), 014021.Google Scholar
Mallet, A., Schekochihin, A. A. & Chandran, B. D. G. 2017 Disruption of sheet-like structures in Alfvenic turbulence by magnetic reconnection. Mon. Not. R. Astron. Soc. 468, 4862–4871.Google Scholar
Matthaeus, W. H. & Lamkin, S. L. 1986 Turbulent magnetic reconnection. Phys. Fluids 29, 2513–2534.Google Scholar
Milligan, R. O., McAteer, R. T. J., Dennis, B. R. & Young, C. A. 2010 Evidence of a plasmoid–looptop interaction and magnetic inflows during a solar flare/coronal mass ejection eruptive event. Astrophys. J. 713, 1292–1300.Google Scholar
Moldwin, M. B. & Hughes, W. J. 1992 On the formation and evolution of plasmoids – a survey of ISEE 3 geotail data. J. Geophys. Res. 97, 19.Google Scholar
Nishizuka, N., Takasaki, H., Asai, A. & Shibata, K. 2010 Multiple plasmoid ejections and associated hard X-ray bursts in the 2000 November 24 flare. Astrophys. J. 711, 1062–1072.Google Scholar
Numata, R. & Loureiro, N. F. 2015 Ion and electron heating during magnetic reconnection in weakly collisional plasmas. J. Plasma Phys. 81 (2), 305810201.Google Scholar
Oka, M., Phan, T.-D., Krucker, S., Fujimoto, M. & Shinohara, I. 2010 Electron acceleration by multi-island coalescence. Astrophys. J. 714 (1), 915.Google Scholar
Olson, J., Egedal, J., Greess, S., Myers, R., Clark, M., Endrizzi, D., Flanagan, K., Milhone, J., Peterson, E., Wallace, J. et al. 2016 Experimental demonstration of the collisionless plasmoid instability below the ion kinetic scale during magnetic reconnection. Phys. Rev. Lett. 116 (25), 255001.Google Scholar
Parker, E. N. 1957 Sweet’s mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509–520.Google Scholar
Pegoraro, F. & Schep, T. J. 1986 Theory of resistive modes in the ballooning representation. Plasma Phys. Control. Fusion 28, 647–667.Google Scholar
Pucci, F. & Velli, M. 2014 Reconnection of quasi-singular current sheets: the ‘ideal’ tearing mode. Astrophys. J. Lett. 780, L19.Google Scholar
Samtaney, R., Loureiro, N. F., Uzdensky, D. A., Schekochihin, A. A. & Cowley, S. C. 2009 Formation of plasmoid chains in magnetic reconnection. Phys. Rev. Lett. 103 (10), 105004.Google Scholar
Servidio, S., Matthaeus, W. H., Shay, M. A., Cassak, P. A. & Dmitruk, P. 2009 Magnetic reconnection in two-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 102 (11), 115003.Google Scholar
Sharma, R., Mitra, D. & Oberoi, D. 2017 On the energization of charged particles by fast magnetic reconnection. Mon. Not. R. Astron. Soc. 470, 723–731.Google Scholar
Shibata, K. & Magara, T. 2011 Solar flares: magnetohydrodynamic processes. Living Rev. Sol. Phys. 8, 6.Google Scholar
Sironi, L. & Spitkovsky, A. 2014 Relativistic reconnection: an efficient source of non-thermal particles. Astrophys. J. Lett. 783, L21.Google Scholar
Sweet, P. A. 1958 The neutral point theory of solar flares. In Electromagnetic Phenomena in Cosmical Physics (ed. Lehnert, B.), IAU Symposium, vol. 6, p. 123.Google Scholar
Tajima, T. & Shibata, K. 2002 Plasma Astrophysics. Perseus.Google Scholar
Tolman, E. A., Loureiro, N. F. & Uzdensky, D. A. 2018 Development of tearing instability in a current sheet forming by sheared incompressible flow. J. Plasma Phys. 84 (1), 905840115.Google Scholar
Uzdensky, D. A. 2011 Magnetic reconnection in extreme astrophysical environments. Space Sci. Rev. 160, 45–71.Google Scholar
Uzdensky, D. A. & Loureiro, N. F. 2016 Magnetic reconnection onset via disruption of a forming current sheet by the tearing instability. Phys. Rev. Lett. 116 (10), 105003.Google Scholar
Uzdensky, D. A., Loureiro, N. F. & Schekochihin, A. A. 2010 Fast magnetic reconnection in the plasmoid-dominated regime. Phys. Rev. Lett. 105 (23), 235002.Google Scholar
Waelbroeck, F. L. 1989 Current sheets and nonlinear growth of the $m=1$ kink-tearing mode. Phys. Fluids B 1, 2372–2380.Google Scholar
Werner, G. R. & Uzdensky, D. A. 2017 Nonthermal particle acceleration in 3D relativistic magnetic reconnection in pair plasma. Astrophys. J. Lett. 843, L27.Google Scholar
Werner, G. R., Uzdensky, D. A., Cerutti, B., Nalewajko, K. & Begelman, M. C. 2016 The extent of power-law energy spectra in collisionless relativistic magnetic reconnection in pair plasmas. Astrophys. J. Lett. 816, L8.Google Scholar
White, R. L. & Hazeltine, R. D. 2017 Analysis of the Hermite spectrum in plasma turbulence. Phys. Plasmas 24 (10), 102315.Google Scholar
Yamada, M., Ji, H., Hsu, S., Carter, T., Kulsrud, R., Bretz, N., Jobes, F., Ono, Y. & Perkins, F. 1997 Study of driven magnetic reconnection in a laboratory plasma. Phys. Plasmas 4, 1936–1944.Google Scholar
Zhang, Q. M. & Ji, H. S. 2014 Blobs in recurring extreme-ultraviolet jets. Astron. Astrophys. 567, A11.Google Scholar
Zhang, T. L., Lu, Q. M., Baumjohann, W., Russell, C. T., Fedorov, A., Barabash, S., Coates, A. J., Du, A. M., Cao, J. B., Nakamura, R. et al. 2012 Magnetic reconnection in the near venusian magnetotail. Science 336, 567.Google Scholar
Zhdankin, V., Uzdensky, D. A., Perez, J. C. & Boldyrev, S. 2013 Statistical analysis of current sheets in three-dimensional magnetohydrodynamic turbulence. Astrophys. J. 771, 124.Google Scholar
Zhou, X., Büchner, J., Bárta, M., Gan, W. & Liu, S. 2015 Electron acceleration by cascading reconnection in the solar corona. I. Magnetic gradient and curvature drift effects. Astrophys. J. 815, 6.Google Scholar
Zocco, A., Loureiro, N. F., Dickinson, D., Numata, R. & Roach, C. M. 2015 Kinetic microtearing modes and reconnecting modes in strongly magnetised slab plasmas. Plasma Phys. Control. Fusion 57 (6), 065008.Google Scholar
Zocco, A. & Schekochihin, A. A. 2011 Reduced fluid-kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18 (10), 102309.Google Scholar
Zong, Q.-G., Fritz, T. A., Pu, Z. Y., Fu, S. Y., Baker, D. N., Zhang, H., Lui, A. T., Vogiatzis, I., Glassmeier, K.-H., Korth, A. et al. 2004 Cluster observations of earthward flowing plasmoid in the tail. Geophys. Rev. Lett. 31, L18803.Google Scholar
Zweibel, E. G. & Yamada, M. 2009 Magnetic reconnection in astrophysical and laboratory plasmas. Annu. Rev. Astron. Astrophys. 47, 291–332.Google Scholar