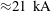Propagation of a nonlinear wave packet driven in a relaxed magnetohydrodynamic plasma

Abstract

We report the observation of a nonlinear wave packet propagating through a relaxed Taylor state in the Swarthmore Spheromak eXperiment (SSX) device. The wave packet is launched by a fast, pulsed, high current (${\approx}21~\text{kA}$) single-turn theta-pinch coil mounted outside the plasma vessel. The theta-pinch coil is energized by discharging a 40 kV, 2 kJ capacitor circuit. The wave packet velocity is super-thermal and super-Alfvénic; its group velocity is more consistent with a whistler pulse than other characteristic velocities. We also observe a fast density pulse which indicates that it is not Alfvénic in nature.

1 Introduction

We have been conducting compression experiments on the relaxed Taylor state in the Swarthmore Spheromak eXperiment (SSX) device (Kaur et al. 2018a , b ). In these experiments, the SSX plasma drifts away from the gun at $40~\text{km}~\text{s}^{-1}$ , stagnates in a closed conducting boundary and then gets compressed by $30\,\%$ . We measure the plasma parameters of the compressed plasma and identify events corresponding to adiabatic compression of the plasma. These events are used to identify the dominant equation of state. In these experiments, we found that the dynamics of weakly collisional SSX plasmas is determined by the parallel Chew–Goldberger–Low (CGL) equations of state. This further suggests that the SSX plasma possesses an anisotropic velocity distribution and has most of its proton energy in the parallel direction with respect to the background magnetic field.

After achieving a compression of $30\,\%$ just due to the inertia of the plasma, we intended to accelerate our plasma to higher velocity such that it hits the end wall with a greater momentum and hence achieves greater compression. We planned to use a series of staged theta-pinch coils. This technique has been used extensively to accelerate and compress axisymmetric plasma structures. In this technique, a set of electrically isolated and independently triggered pinch coils are used to translate and accelerate field reversed configurations (FRCs). In compression experiments on the Inductive Plasma Accelerator (IPA) device, two axisymmetric FRCs were accelerated to $300~\text{km}~\text{s}^{-1}$ into a conical section using pinch coils and merged with complete magnetic FRC reconnection in the middle cylindrical section of the device (Votroubek et al. 2008; Slough, Votroubek & Pihl 2011). The merged plasmoid was then compressed to heat the ions to kilovolt ion temperatures, which was accompanied by an increase in the plasma radius and a strong neutron flux detected by scintillator-based detectors employed at the axial midplane.

Using a similar approach at TAE Technologies, two oppositely moving axisymmetric FRCs are translated in a straight cylinder to a middle section of the device and merged magnetically (Binderbauer et al. 2010; Tuszewski et al. 2012). During the merging process, more than $60\,\%$ of the kinetic energy is converted into plasma thermal energy and the rest goes into an increase in the magnetic energy. The FRC poloidal flux was found to increase by a factor of 10 during merging. Substantial plasma heating (exceeding 0.5 keV) due to conversion of most of kinetic energy into thermal energy and a long FRC lifetime was observed. Thermal energy was transferred to heat the ions (total temperature is $\backsimeq 5.5T_{e}$ ).

In all these experiments, axisymmetric structures were generated and accelerated. Thus far, pulsed coil acceleration of a non-axisymmetric structure has not been tried. In our experiments, we generate an axisymmetric structure which then relaxes to a stable non-axisymmetric Taylor state (Gray, Brown & Dandurand 2013). The benefit of using a non-axisymmetric Taylor state is that it is the minimum energy relaxed state in magnetohydrodynamics (MHD). As we mentioned earlier, we originally aimed to accelerate these non-axisymmetric Taylor states to high velocities and then compress to obtain a stable, dense hot plasma which could further be used as a target for fusion applications.

We designed and installed a pulsed theta-pinch coil on our device initially to accelerate and compress the Taylor state. Instead, the main physical effect is the generation of a large amplitude magnetic structure propagating along the background Taylor state field, and reflecting off the back wall. The velocity of the propagating magnetic structure is super-Alfvénic (measured using a linear array of ${\dot{B}}$ probes) and is more consistent with the whistler wave group velocity than Alfvén speed.

The remainder of the paper is organized as follows. In § 2, we review the theory of whistler waves and kinetic Alfvén waves describing expressions for their respective group velocities (later used for calculating their respective values). In § 3, we provide an overview of prior laboratory experiments conducted on whistler waves. In § 4, we describe the experimental set-up and the pinch coil assembly followed by a discussion on our two principal diagnostics: a HeNe laser interferometer for density measurements and a magnetic probe array for magnetic structure and time-of-flight measurements. In § 5, we present our experimental results followed by a brief discussion and conclusion in § 6.

2 Theory

Whistler waves are dispersive electromagnetic waves mediated by the electrons in a magnetized plasma. These are right-handed waves that propagate between the ion and electron cyclotron frequencies. Therefore, the propagation characteristics of the whistler mode may be easily understood by considering the R-wave dispersion relation. The index of refraction for the right-hand polarized mode (Gurnett & Bhattacharjee 2005; Bellan 2006) is

(2.1) $$\begin{eqnarray}\displaystyle n^{2}=\frac{c^{2}k^{2}}{\unicode[STIX]{x1D714}^{2}}=1-\frac{\unicode[STIX]{x1D714}_{pe}^{2}/\unicode[STIX]{x1D714}^{2}}{1-\unicode[STIX]{x1D714}_{ce}/\unicode[STIX]{x1D714}}-\frac{\unicode[STIX]{x1D714}_{pi}^{2}/\unicode[STIX]{x1D714}^{2}}{1+\unicode[STIX]{x1D714}_{ci}/\unicode[STIX]{x1D714}}, & & \displaystyle\end{eqnarray}$$

where, $\unicode[STIX]{x1D714}$ is the wave frequency, $k$ is the wavenumber, $c$ is the speed of light, $\unicode[STIX]{x1D714}_{pe}$ and $\unicode[STIX]{x1D714}_{pi}$ are the electron and ion plasma frequencies, respectively, while $\unicode[STIX]{x1D714}_{ce}$ and $\unicode[STIX]{x1D714}_{ci}$ are the electron cyclotron and ion cyclotron frequencies, respectively. Since for whistler waves, the frequency of interest is well above the ion cyclotron frequency, the third term on the right-hand side of (2.1) can be dropped and the dispersion relation for whistler waves becomes,

(2.2) $$\begin{eqnarray}\displaystyle \frac{c^{2}k^{2}}{\unicode[STIX]{x1D714}^{2}}=\frac{\unicode[STIX]{x1D714}_{pe}^{2}/\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D714}_{ce}/\unicode[STIX]{x1D714}-1}. & & \displaystyle\end{eqnarray}$$

These waves propagate along the background magnetic field within a cone given by $cos\unicode[STIX]{x1D703}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{ce}$ , so for $\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D714}_{ce}$ , they can propagate at almost any angle with respect to $\boldsymbol{B}_{0}$ . In the limit of $\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D714}_{ce}$ , the dispersion relation can be rewritten as follows:

(2.3) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{ce}\left(\frac{ck}{\unicode[STIX]{x1D714}_{pe}}\right)^{2}. & & \displaystyle\end{eqnarray}$$

From the above equation, it is clear that for whistlers, the frequency varies nonlinearly with the wavenumber, so the group velocity $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k$ also has a dependence on $k$ (and therefore also on $\unicode[STIX]{x1D714}$ ):

(2.4) $$\begin{eqnarray}\displaystyle v_{g}=2c\frac{\sqrt{\unicode[STIX]{x1D714}\unicode[STIX]{x1D714}_{ce}}}{\unicode[STIX]{x1D714}_{pe}}. & & \displaystyle\end{eqnarray}$$

As the group velocity is proportional to the square root of the frequency, the higher frequencies propagate faster than the lower frequencies.

In addition to whistler waves, the plasma also supports other electromagnetic modes in magnetized plasma – the most ubiquitous mode being shear Alfvén waves. Shear Alfvén waves are low frequency electromagnetic waves that propagate below the ion cyclotron frequency. The shear Alfvén waves exhibit two different propagating characteristics depending on the dimensionless parameter $\bar{\unicode[STIX]{x1D6FD}}=v_{te}^{2}/(\unicode[STIX]{x1D714}/k_{\Vert })^{2}$ , where $v_{te}$ is the electron thermal velocity, $\unicode[STIX]{x1D714}$ is the frequency of the wave and $k_{\Vert }$ is the wavenumber parallel to the ambient magnetic field. For $\bar{\unicode[STIX]{x1D6FD}}\gg 1$ , the shear Alfvén wave is called the kinetic Alfvén wave (Gekelman et al. 1997, 2011) while for $\bar{\unicode[STIX]{x1D6FD}}\ll 1$ , the shear Alfvén wave is referred to as the inertial Alfvén wave (Gekelman et al. 1997, 2011). In our experiment $\bar{\unicode[STIX]{x1D6FD}}\gg 1$ and the dispersion relation for the kinetic Alfvén wave is given by (Stasiewicz et al. 2000)

(2.5) $$\begin{eqnarray}\frac{\unicode[STIX]{x1D714}}{k_{\Vert }}=v_{A}\sqrt{1+k_{\bot }^{2}\unicode[STIX]{x1D70C}_{s}^{2}\left(1+\frac{T_{i}}{T_{e}}\right)-\bar{\unicode[STIX]{x1D714}}^{2}\left(1+k_{\bot }^{2}\unicode[STIX]{x1D70C}_{s}^{2}\frac{T_{i}}{T_{e}}\right)},\end{eqnarray}$$

where $\bar{\unicode[STIX]{x1D714}}$ is the wave frequency normalized by the ion cyclotron frequency ( $\unicode[STIX]{x1D714}_{ci}$ ), $k_{\bot }$ is perpendicular wavenumber, $T_{i}$ and $T_{e}$ are the ion and electron temperature, respectively. $\unicode[STIX]{x1D70C}_{s}$ is the ion sound gyroradius ( $=\sqrt{T_{e}/m_{i}}/\unicode[STIX]{x1D714}_{ci}$ ) and $v_{A}$ is the Alfvén speed, given by

(2.6) $$\begin{eqnarray}\displaystyle v_{A}=\frac{B}{\sqrt{4\unicode[STIX]{x03C0}n_{i}m_{i}}}, & & \displaystyle\end{eqnarray}$$

where $m_{i}$ , $n_{i}$ and $B$ represent mass of ion, plasma density and magnetic field, respectively.

The kinetic Alfvén wave usually propagates with a group velocity predominantly directed along the ambient magnetic field lines. The parallel group velocity of kinetic Alfvén wave is given by

(2.7) $$\begin{eqnarray}v_{g\Vert _{\text{KAW}}}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}k_{\Vert }}=\frac{v_{A}}{1+k_{\bot }^{2}\unicode[STIX]{x1D70C}_{s}^{2}\left(1+{\displaystyle \frac{T_{i}}{T_{e}}}\right)}\left\{1+k_{\bot }^{2}\unicode[STIX]{x1D70C}_{s}^{2}\left(1+\frac{T_{i}}{T_{e}}\right)-\bar{\unicode[STIX]{x1D714}}^{2}\left(1+k_{\bot }^{2}\unicode[STIX]{x1D70C}_{s}^{2}\frac{T_{i}}{T_{e}}\right)\right\}^{3/2},\end{eqnarray}$$

where $v_{g_{\Vert _{\text{KAW}}}}$ is the parallel group velocity.

From equation (2.7), it is clear that $v_{g_{\Vert _{\text{KAW}}}}$ of the kinetic Alfvén wave decreases as the frequency approaches the ion cyclotron frequency. On the other hand, an increase in finite perpendicular wavenumber increases $v_{g_{\Vert _{\text{KAW}}}}$ . However, when the perpendicular wavelength is much greater than the ion sound gyroradius $(k_{\bot }^{2}\unicode[STIX]{x1D70C}_{s}^{2}\ll 1)$ and the wave frequency is much lower than the ion cyclotron frequency $(\bar{\unicode[STIX]{x1D714}}^{2}\ll 1)$ , the parallel group velocity becomes approximately equal to the Alfvén speed.

3 Overview of prior experiments of whistler waves in the laboratory

Whistler waves were originally observed in audio detection of radio waves a century ago due to their characteristic falling whistle tone (Preece 1894; Storey 1953; Barkhausen 1919). Laboratory studies of whistler waves were pioneered by R. L. Stenzel at UCLA. In over 50 papers, the Stenzel team carefully mapped out dispersion relations, phases and group velocities of whistler waves (Stenzel 1976, 1999). The plasma device used a large BaO cathode (0.5 m) to produce a magnetized ( $0<B_{0}<150~\text{G}$ ), cold ( $T_{e}\leqslant 2~\text{eV}$ , $T_{i}\leqslant 0.2~\text{eV}$ ), low density $n_{e}\leqslant 10^{12}~\text{cm}^{-3}$ plasma. Coherent whistler waves and bursts were excitated by either magnetic coils (Stenzel, Urrutia & Rousculp 1993; Rousculp, Stenzel & Urrutia 1995), or electrodes immersed in an afterglow plasma (Urrutia & Stenzel 1989; Urrutia, Stenzel & Rousculp 1994).

In the case of a magnetic coil antenna, when a short burst of current is applied, a detached structure is formed that propagates away from the antenna at the whistler group velocity (Stenzel & Urrutia 1990; Stenzel 1999). In some cases, the structure is a nearly spherical vortex. It can be demonstrated that the current density $(J)$ in these structures is parallel to the wave magnetic field $(\boldsymbol{B}_{\text{wave}})$  (i.e.  $\boldsymbol{J}\propto \boldsymbol{B}_{\text{wave}}$ ) so that the structures can be thought of as force free in the context of electron MHD (EMHD). A simple loop antenna launches whistler packets in both directions, with opposite EMHD helicity.

In a sequence of over a dozen papers, the Stenzel group studied pulsed currents carried by whistler structures (Urrutia & Stenzel 1989; Stenzel et al. 1993). In these experiments, the background magnetic field was very low ( $B_{0}\leqslant 20~\text{G}$ ) so the ions were unmagnetized. The experiments were performed in the afterglow discharge so that the cathode currents were not present. The full three-dimensional magnetic field $\boldsymbol{B}(\boldsymbol{r},t)$ was mapped point-by-point from more than $10^{5}$ highly repeatable shots, so that the current density could be calculated directly by Ampere’s law, $\unicode[STIX]{x1D707}_{0}\boldsymbol{J}(\boldsymbol{r},t)=\unicode[STIX]{x1D735}\times \boldsymbol{B}(\boldsymbol{r},t)$ . Measurements showed that indeed contours of components of $\boldsymbol{B}$ and $\boldsymbol{J}$ had very similar topologies.

When high currents are applied to the antenna, nonlinear effects are observed (Urrutia & Stenzel 1991, 1996). In some cases, wave fields can exceed the background field $\boldsymbol{B}_{0}$ (Stenzel, Urrutia & Strohmaier 2006), and the field energy density far exceeds the particle thermal energy ( $\tilde{\boldsymbol{B}}^{2}/2\unicode[STIX]{x1D707}_{0}\cong 10^{4}~\text{nkT}$ ) (Urrutia & Stenzel 1991). In other words, the intense electromagnetic pulse from the antenna rapidly heats the electrons. A high conductivity current channel produced by the hot electrons allows the nonlinear wave to penetrate anomalously into the collisional background plasma (Urrutia & Stenzel 1991). We believe that this mechanism could be at play during our experiments with the theta-pinch coil.

4 Experimental set-up

Parcels of MHD plasma are produced using a magnetized coaxial plasma gun located at one end of the linear device, as shown in figure 1. The diameter of the inner electrode of the gun is 6.2 cm and the outer electrode (i.e. flux conserver) diameter is 15 cm. More details about the plasma gun can be found in earlier publications (Geddes, Kornack & Brown 1998; Brown & Schaffner 2014, 2015). At the other end of the linear chamber, a closed, tungsten-lined copper can, referred to here as a stagnation flux conserver (SFC), is installed. The SFC is 30 cm long and has the same inner diameter as the outer flux conserver of the gun. A 1 m long quartz tube (diameter = 15 cm) is installed in between the gun and the SFC to accommodate pinch coils in these experiments. One pinch coil has been installed on the glass tube as shown in figure 1. The glass tube is partially covered with a copper flux conserving shell having a long magnetic soak time ( ${>}260~\unicode[STIX]{x03BC}\text{s}$ ) to provide some flux conservation to the magnetized plasma in its relaxation phase. We maintain a good vacuum using a cryopump.

Figure 1. A schematic of the experimental set-up. A glass tube is added in between the gun and the stagnation flux conserver (SFC) and is covered with a 53.3 cm long copper flux conserving shell near the gun. A high permeability Permendur rod is installed at the centre of the inner electrode shell. Two principal plasma diagnostics are located in the SFC. The plasma density, $n_{e}$ , is measured using HeNe laser interferometry along a horizontal chord. The long ${\dot{B}}$ probe array is aligned along the axis of the SFC. The red lines on the magnetic probe array represent the locations of the ${\dot{B}}$ probes.

Tungsten-lined coaxial electrodes of the gun are cleaned by generating a He glow discharge before experiments to obtain good wall conditions and to maintain a low-impurity plasma. A strong magnetic field ( $\backsim 1~\text{T}$ ) is generated in the inner electrode using an external electromagnet and a strong ferromagnetic core. Hydrogen gas is puffed into the annular region between the two electrodes using gas puff valves. A voltage pulse ( ${\approx}4~\text{kV},8~\text{kJ}$ ) is applied between the two electrodes which ionizes the gas and causes a high current ( $\backsim 100~\text{kA}$ ) to flow through the plasma. $\boldsymbol{J}\times \boldsymbol{B}$ forces accelerate the plasma out of the gun and a toroidal self-consistent magnetic object, called a spheromak (Geddes et al. 1998), is formed. The confining magnetic field is convected along with the drifting spheromak and is sustained entirely by the currents flowing in the plasma.

4.1 Description of the theta-pinch coil assembly

The theta-pinch coil assembly is made up of various high voltage components along with the theta-pinch coil itself. In this section, we will discuss about these components one by one.

4.1.1 Pinch coil

In order to accelerate the Taylor state moving at $40~\text{km}~\text{s}^{-1}$ (i.e. $4~\text{cm}~\unicode[STIX]{x03BC}\text{s}^{-1}$ ), we aimed to keep the quarter-cycle rise time ( $t_{1/4}\approxeq (\unicode[STIX]{x03C0}/2)\sqrt{LC}$ ) near $1~\unicode[STIX]{x03BC}\text{s}$ . Our capacitance is $3~\unicode[STIX]{x03BC}\text{F}$ . Therefore, the design inductance of the single-turn coil must be $\approxeq 135~\text{nH}$ . We designed a 10.2 cm wide (i.e. axial length) single-turn coil with diameter as 15.2 cm using a copper sheet of thickness 2.5 mm.

Figure 2. A schematic of the high voltage module showing the connections of the switches and the capacitor to the theta-pinch coil. The line and arrows in the red colour show the path of the current and its direction when the switch fires, whereas the same in the blue colour corresponds to the crowbar firing.

To reduce the inductance of the rest of the circuit, we made use of identical, multiple coaxial cable connections from the capacitor to the collector plates of the pinch coil. Each collector plate has nine 90 cm long coaxial cable connections. These plates are 15.2 cm wide to enable multiple coaxial cable connections and are tapered to 10.2 cm near the coil. The inductance due to the collector plates is below 15 nH. Total inductance of the nine $RG213$ coaxial cables is ${\approx}27~\text{nH}$ . The quarter-cycle rise time for the entire circuit comes out to be $\approxeq 1~\unicode[STIX]{x03BC}\text{s}$ , which also determines the required delay between the switch and the crowbar.

4.1.2 Electrical circuit

A high voltage circuit has been developed for energizing the pinch coil and its schematic is shown in figure 2. The capacitor is charged through a charging resistor using a high-voltage (HV) power supply made by TDK Lambda, essentially a current source, which can charge the capacitor to 40 kV. To protect the power supply, we use series and parallel combinations of high voltage diodes; each diode is rated up to 15 kV. The capacitor is connected to the coil through a HV pseudo-spark switch, often known as Buchkov switch (Buchkov et al. 2009; Slough et al. 2009) that can deliver current up to 200 kA at current rise rates up to $10^{12}~\text{A}~\text{s}^{-1}$ . We use two of these switches in the circuit; one of these is used as a switch while the other is used as a crowbar to prevent ringing (Slough et al. 2009). A schematic of the electronic circuit is shown in figure 3. For safety purposes, there is a parallel circuit to dump all the charge on the capacitor in a fraction of a second through a dump resistor. The dump circuit makes use of a high voltage Ross relay rated to 40 kV.

Figure 3. A schematic of the electronic circuit used for generating a pulsed magnetic field using the theta-pinch coil. Switch and crowbar are the Buchkov switches which are capable of operating for more than 20 000 shots.

Each switch has a dedicated heater voltage circuit and requires 5–15 min of heating before the operation. The switches are triggered by using a high voltage pulse of 1.6 kV. The high voltage pulses are applied using a pulsed circuit (provided by Tri-Alpha Energy Technologies). The timing between the switch and the crowbar is adjusted using a Stanford Research Systems made delay generator (DG535) capable of operating at nanosecond precision. The output of the delay generator is converted into an optical pulse which triggers the Tri-Alpha Energy pulsed circuit for providing trigger to the switch and the crowbar.

The gap between the two collector plates of the pinch coil is 3 mm. To prevent arcing or breakdown in between the collector plates, we use a combination of high voltage insulators. The insulation includes multiple alternate sheets of 5 mm thick Kapton and polyethylene with paper sheets in between to prevent any space charge build-up. The entire combination is designed to work up to a dc voltage of 80 kV.

The switch and the crowbar along with their connections to the HV capacitor are immersed in a high voltage insulation oil. The HV oil is STO-50 dielectric silicone fluid and has very low vapour pressure. It prevents high voltage discharge/arcing and is inert to virtually all metals, plastics and rubbers.

4.2 Diagnostics

For these experiments, we rely on two principal diagnostics. We measure the line averaged electron density of the plasma along a horizontal chord with a 632.8 nm HeNe laser Mach–Zehnder interferometer. Changes in plasma electron density introduce a change in the plasma frequency:

(4.1) $$\begin{eqnarray}\unicode[STIX]{x1D714}_{pe}=\sqrt{\frac{4\unicode[STIX]{x03C0}e^{2}n_{e}}{m_{e}}}.\end{eqnarray}$$

The refractive index of the plasma is related to the plasma frequency:

(4.2) $$\begin{eqnarray}n^{2}=1-\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}_{L}^{2}},\end{eqnarray}$$

where $\unicode[STIX]{x1D714}_{L}$ is the frequency of the incident laser beam. We can then use the line integrated phase difference introduced in the scene beam of the interferometer to determine the line averaged plasma density over the path of the laser. This is done by passing the reference beam through a quarter-wave plate to circularly polarize it and then recombining the scene beam and reference beam. The recombined beam is passed through a Wollaston prism to generate two outputs $90^{\circ }$ out of phase with each other, and the intensity of each of the two output beams is measured by using two separate photodetectors.

Along with the laser interferometry, we use a long ${\dot{B}}$ probe array (encased in a quartz glass tube) along the axis of the SFC. The long probe is aligned almost along the axis of the SFC. The ${\dot{B}}$ probe has densely spaced (1.5 cm), single turn, two directional probes located inside the SFC, employed for determining the Taylor state structure along the axis as well as its time of flight velocity. The array also has few three directional probes, which are co-located with the interferometry chord. These three directional probes are used to measure the local vector magnetic field.

Apart from these two diagnostics, we use a 100-turn Rogowski coil to measure the current flowing through the theta-pinch coil. It is mounted on the live end of the theta-pinch coil collector plate. The Rogowski coil is equipped with an RC integrator and showed a linear frequency response from 200 kHz to 2 MHz.

5 Results and discussion

Plasma parameters such as the electron density and magnetic field are measured in the compression volume using HeNe laser interferometry and a linear ${\dot{B}}$ probe array, respectively. In these experiments, the theta-pinch coil is mounted 18 cm away from the front end of the SFC and it is 32 cm away from the interferometry port. This distance was selected: (i) to avoid driving eddy currents in the vessel walls due to coil firing, and (ii) to be able to easily detect the effect of the firing of the coil on the Taylor states. We let the plasma reach the SFC and stagnate against the end wall. Then we carry out a delay scan by firing the coil at different times with respect to the time it takes to reach the end wall. In this section, we will discuss about the results obtained using the density and the magnetic field data after firing the theta-pinch coil.

Magnetic field embedded in the structure in the compression volume is found to be ${\approx}300{-}400~\text{G}$ . Time-of-flight (ToF) velocity of the plasma from one probe location to the next is determined by direct comparison of the magnetic field structures as well as by carrying out a cross-correlation analysis. With the glass boundary, the typical flow velocity of the plasma is found to be ${\approx}40~\text{km}~\text{s}^{-1}$ , accompanied by a fast plasma ( ${\geqslant}60~\text{km}~\text{s}^{-1}$ ) at the leading edge. The bulk of the plasma fills the SFC at ${\approx}56~\unicode[STIX]{x03BC}\text{s}$ .

Immediately after the coil fires, we observe a magnetic wave packet/structure propagating down the SFC with a mean velocity of $37~\text{km}~\text{s}^{-1}$ . A couple of microseconds later, we see the same magnetic structure moving back towards the gun at $25~\text{km}~\text{s}^{-1}$ . After a careful analysis, we found that the magnetic structure gets reflected back from the end wall of the SFC. We do not observe this reflection for the shots in which we do not fire the theta-pinch coil. Velocity of the reflected structure is lower as compared to the forward traveling as the plasma is accelerated only in the beginning due to the $\boldsymbol{J}\times \boldsymbol{B}$ forces. After that, the structure keeps on moving away from the gun due to its inertia and it’s velocity gradually decreases.

A typical magnetic field signal obtained using a set of six axial ${\dot{B}}$ probes (oriented in the same direction, i.e. $B_{x}$ ) after firing the pinch coil is shown in figure 4. In this shot, the switch was fired at $58~\unicode[STIX]{x03BC}\text{s}$ and the crowbar was fired with a delay of $0.8~\unicode[STIX]{x03BC}\text{s}$ . Corresponding to these settings for the switches, the coil current peaks at $\simeq 60~\unicode[STIX]{x03BC}\text{s}$ . In figure 4, we can clearly see two counter-propagating signals. For the data presented in this paper, we charged the capacitor to different voltages 25 kV, 30 kV and 33 kV and kept the gun parameters (such as direction and magnitude of stuffing flux, gas delay and gun voltage) the same for each of the capacitor voltages.

Figure 4. A typical $x$ -component of the magnetic field obtained by using six ${\dot{B}}$ probes at different axial locations away from the SFC wall. Here, the probe located at 9 cm away from the wall is the farthest probe with respect to the gun whereas the one at 16.5 cm from the wall is the closest to the gun and the interferometry chord. The black colour time trace corresponds to the coil current flowing through the theta-pinch coil. High voltage capacitor is charged to 33 kV and the coil current peaks at approximately $60~\unicode[STIX]{x03BC}\text{s}$ . The uncertainty in the magnetic field measurements is ${<}10\,\%$ and accounts for the errors due to the numerical integration.

The measured velocity is plotted versus the predicted group velocity (either whistler or Alfvén) for both forward and reflected waves and is shown in figure 5 as three probability distributions (each contains $\simeq 100$ independent measurements) corresponding to three different capacitor voltages. Whistler wave and kinetic Alfvén wave group velocities are calculated using equation (2.4) and (2.7), respectively corresponding to the background plasma density and magnetic field. The frequency ( $\unicode[STIX]{x1D714}$ ) for calculating these group velocities is obtained from the Rogowski coil signal. A finite perpendicular wavelength increases the parallel group velocity of kinetic Alfvén wave, $v_{g_{\Vert _{\text{KAW}}}}$ . For example, according to equation (2.7) at $k_{\bot }\unicode[STIX]{x1D70C}_{s}=2$ , $v_{g_{\Vert _{\text{KAW}}}}=1.4v_{A}$ , while for $k_{\bot }\unicode[STIX]{x1D70C}_{s}=3$ , $v_{g_{\Vert _{\text{KAW}}}}=2.1v_{A}$ . We do not have the flexibility to measure the perpendicular wavenumber. Therefore, in the absence of $k_{\bot }$ measurements, we have approximated the kinetic Alfvén wave group velocity to $\approxeq 2v_{A}$ .

Figure 5. Contour plots for the velocity distribution of $\simeq 300$ measurements corresponding to different capacitor voltages, showing the comparison of the measured velocity (along $y$ -axis) with respect to the whistler wave group velocity (along the $x$ -axis) for the forward and backward travelling magnetic structure in (a,b), and the same with respect to the kinetic Alfvén waves (along the $x$ -axis) in (c,d), respectively. In each panel, the dark blue colour corresponds to the most prominent measured and corresponding calculated whistler (or Alfvén) velocity at 25 kV, the green colour at 30 kV and the red colour at 33 kV (computed using background plasma density and magnetic field values). In each panel, the average velocities (measured and computed) have been marked and mentioned along with the error bars.

The vertical spread in the data corresponds to the spread in the ToF velocity (i.e. distance per time lag) measured using six magnetic probes located at different axial positions in the stagnation flux conserver (see figure 4). Each plasma shot provides us with five values of velocity for the forward travelling magnetic structure and five for the reflected structure. If the measured velocity is equal to either the whistler velocity or Alfvén velocity, then the mean in the spread will be closer to the diagonal line. The large vertical spread in the measured velocity could be due to several possible reasons: (i) one of the reasons could be the different voltages applied to the pinch coil. For lower capacitor voltages (or lower currents flowing through the coil), the velocity distribution is near the bottom. Whereas for higher currents, the overall velocity distribution seems to shift towards higher velocities. This is also reflected in figure 5. The gun generated plasma has a small shot-to-shot variation, which could also contribute to this spread. In addition, the twisted Taylor state has a small, but finite, azimuthal (rotational) velocity which can vary with each shot. Since it is a non-axisymmetric structure so its coupling to the pinch coil magnetic field (symmetric) could vary azimuthally. Our time of flight probes utilize just one component of magnetic field so this azimuthal variation may introduce some uncertainty.

Figure 6. The average plasma density obtained from 8 shots for which the theta-pinch coil was fired at $58~\unicode[STIX]{x03BC}\text{s}$ and the current flowing through the coil peaks at $60~\unicode[STIX]{x03BC}\text{s}$ . The fiducial point A corresponds to the time when the Taylor state reaches the interferometry chord, B to the noise due to pinch coil firing, C to the fast density pulse and D corresponds to the second reflected density pulse. The fast density pulse (indicated by point C) is observed right after firing the coil in the interferometer cord which is located 32 cm away from the pinch coil and is 19 cm away from the back end of the SFC. The uncertainty in the density measurement is ${<}10\,\%$ .

These data correspond to different plasma shots taken by keeping the gun parameters same but at three different values of magnetic field generated by the theta-pinch coil, i.e. 1.3 kG, 1.5 kG and 1.7 kG corresponding to three different capacitor voltages, i.e. 25 kV, 30 kV and 33 kV. We observe that the mean velocity of the magnetic structure increases with an increase in the current flowing through the pinch coil. The theta-pinch coil magnetic field is, in all of the cases, more than four times the magnetic field embedded in the plasma. We find that the observed forward velocity is closer to the whistler group velocity than the Alfvén group velocity.

In addition to the magnetic wave packet, we observe a fast density pulse propagating through the SFC after we fire the pinch coil. The fast density pulse is detected using the HeNe laser interferometer. An average density trace from 8 shots taken under the same conditions is shown in figure 6. Time of flight velocity of the fast density pulse is also measured. In this case, ToF velocity is measured (not shown in this paper) from the ratio of the axial distance of the coil from the location of the density measurement chord to the delay in the observation of the fast density pulse with respect to the time when the current flowing through the coil peaks. The coil is mounted 32 cm away from the density measurement chord. The time of flight velocity measured using density pulses comes out to be close to the ion sound speed and is likely unrelated to the whistler pulse. We compared the velocities obtained using both time of fight methods; using density pulses and the magnetic probe signal. The time of flight velocity from the density pulse is different and faster than that obtained from the magnetic probe analysis and could be addressed separately in a future article.

There could be many possible explanations for the occurrence of these super-Alfvénic structures. We discuss about few of these here. Super-Alfvénic pulses have been measured in the solar wind and magnetosphere. In one set of the observations, the super-Alfvénic pulses, referred to as the magnetosonic shocklets (Stasiewicz et al. 2003), have been found to move at $250~\text{km}~\text{s}^{-1}$ , seven times faster than the Alfvén speed. In another observation of field-aligned ion beams near large amplitude magnetic field fluctuations in the terrestrial foreshock, it is found that these structures propagate (in the plasma frame) away from the bow shock toward the upstream (sunward) side of the short–large amplitude magnetic structures (Wilson et al. 2013). We do not claim that the magnetic structures observed in our experiments are same as observed by the space plasma community; however, these space observations are suggestive of possible mechanisms in our experiment.

In addition, there are a few more possible explanations for the observed discrepancy in the propagation speed of the magnetic structures. First, from figure 4 we see that the pinch coil pulse peaks to 20 kA, so the local magnetic field generated by the coil is $\simeq 1.7~\text{kG}$ ( $B=\unicode[STIX]{x1D707}_{0}I/2R$ ). This far exceeds the magnetic field embedded in the Taylor state, which is $\simeq 400~\text{G}$ . It is likely that the whistler pulse propagates in a large axial field once formed.

Second, we only measure the line averaged density in the SFC and have not measured $T_{e}$ . It is possible that the large pinch coil pulse modifies the background plasma, as was observed in the Stenzel experiments (Urrutia & Stenzel 1991), and provides a nonlinear enhancement to the propagation speed.

Finally, the theta-pinch coil could launch several modes in the plasma as it is pulsed only for a half-cycle, which means whistler wave and kinetic Alfvén wave calculations should take into account all the different frequencies excited. However to compute these group velocities, we approximate the pulse period to be four times the quarter-cycle rise time of the current flowing through the coil, observed in the Rogowski coil. In addition, we have approximated the kinetic Alfvén wave group velocity to $\approxeq 2v_{A}$ by assuming $k_{\bot }\unicode[STIX]{x1D70C}_{s}\lesssim 3$ in the absence of $k_{\bot }$ measurements. However, for higher values of $k_{\bot }\unicode[STIX]{x1D70C}_{s}$ , the group velocity of the kinetic Alfvén wave would be ${>}2v_{A}$ . A more detailed analysis would involve both the nonlinear effects of the pinch coil current and the propagation of multiple frequencies in the pulse. This analysis will be performed at a later time.

6 Summary

We measure the propagation of a nonlinear wave packet through a relaxed Taylor state equilibrium. The wave packet is driven by passing a high current through a pinch coil mounted outside the vacuum vessel, but coaxial with the glass tube. In these experiments, we observe a wave packet propagating along the background magnetic field, into the SFC and then getting reflected back at the end wall. The forward and backward time of flight velocity of the wave packet is measured using densely spaced ${\dot{B}}$ probes. The wave packet is found to move faster at higher currents flowing through the pinch coil. The measured velocity is compared with the characteristic velocities of the magnetized plasma such as the group velocity of the whistler waves and the kinetic Alfvén waves, and is found to be faster than both of the characteristic wave velocities. However, the disagreement between the measured velocity of wave packet and the whistler velocity is less when compared with the group velocity of kinetic Alfvén waves. In addition, the measured velocity is found to increase with an increase in the current flowing through the pinch coil.