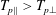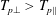1 Introduction
In situ observations in the weakly collisional solar wind (Marsch Reference Marsch2006) indicate the presence of apparent bounds on different particle parameters. The observed bounds on the temperature anisotropy of protons (Gary et al. Reference Gary, Skoug, Steinberg and Smith2001; Kasper et al. Reference Kasper, Lazarus, Gary, Szabo, Velli, Bruno and Malara2003; Hellinger et al. Reference Hellinger, Trávníček, Kasper and Lazarus2006; Hellinger & Trávníček Reference Hellinger and Trávníček2014), alpha particles (Maruca, Kasper & Gary Reference Maruca, Kasper and Gary2012), electrons (Štverák et al. Reference Štverák, Trávníček, Maksimovic, Marsch, Fazakerley and Scime2008), and/or on the differential velocity between ion species (Bourouaine et al. Reference Bourouaine, Verscharen, Chandran, Maruca and Kasper2013; Matteini et al. Reference Matteini, Hellinger, Schwartz and Landi2015) and the differential velocity between different electron species (heat flux driven instabilities) (Gary et al. Reference Gary, Neagu, Skoug and Goldstein1999) are often compatible with the constraints imposed by kinetic plasma instabilities. Some observations also indicate that there are enhanced levels of fluctuations near the apparent bounds (Bale et al. Reference Bale, Kasper, Howes, Quataert, Salem and Sundkvist2009; Wicks et al. Reference Wicks, Matteini, Horbury, Hellinger and Roberts2013; Lacombe et al. Reference Lacombe, Alexandrova, Matteini, Santolík, Cornilleau-Wehrlin, Mangeney, de Conchy and Maksimovic2014), supporting the interpretation that these bounds are imposed by the kinetic instabilities.
The evolution of the solar wind particle properties depends on the processes that are active. For instance, Alfvén ion cyclotron waves heat the ions in the direction perpendicular to the ambient magnetic field (Hollweg & Isenberg Reference Hollweg and Isenberg2002; Hellinger et al. Reference Hellinger, Velli, Trávníček, Gary, Goldstein and Liewer2005), whereas plasma turbulence generates a range of particle temperature anisotropies and even non-gyrotropies (Servidio et al. Reference Servidio, Valentini, Perrone, Greco, Califano, Matthaeus and Veltri2015). The solar wind expansion tends to generate particle temperature anisotropies and influences as well the differential streaming between different species. Matteini et al. (Reference Matteini, Landi, Hellinger, Pantellini, Maksimovic, Velli, Goldstein and Marsch2007) investigated the radial evolution of the proton temperature anisotropy in the fast solar wind in the beta-anisotropy plane: below 1 a.u., protons follow an anticorrelation between the proton beta and the proton temperature anisotropy (cf. Marsch, Ao & Tu Reference Marsch, Ao and Tu2004). This behaviour is not compatible with the double-adiabatic prediction (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956) and indicates the presence of proton heating, likely owing to the turbulent cascade (Cranmer et al. Reference Cranmer, Matthaeus, Breech and Kasper2009; Hellinger et al. Reference Hellinger, Trávníček, Štverák, Matteini and Velli2013). Beyond 1 a.u., the results of Matteini et al. (Reference Matteini, Landi, Hellinger, Pantellini, Maksimovic, Velli, Goldstein and Marsch2007) indicate that the behaviour of protons changes; the system seems to follow in the beta-anisotropy plane a marginal stability path with respect to the proton fire hose instabilities.
Results similar to the observations of Matteini et al. (Reference Matteini, Landi, Hellinger, Pantellini, Maksimovic, Velli, Goldstein and Marsch2007) are seen in numerical simulations using the expanding box model (Matteini et al. Reference Matteini, Landi, Hellinger and Velli2006; Hellinger & Trávníček Reference Hellinger and Trávníček2008): the expansion drives the parallel temperature anisotropy and fire hose instabilities limit the accessible temperature anisotropy. These results were, however, obtained for the strictly radial ambient magnetic field, whereas the magnetic field in the solar wind is generally oblique with respect to the radial direction and rotates towards a transverse direction (Parker Reference Parker1958). For a solar wind magnetic field which is sufficiently oblique relative to the radial direction from the Sun, the double-adiabatic approximation predicts generation of the perpendicular temperature anisotropy (Matteini et al. Reference Matteini, Hellinger, Landi, Trávníček and Velli2012). In this paper we investigate the role of the oblique magnetic field on the fire hose instabilities using two-dimensional hybrid expanding box simulations. The paper is organized as follows: § 2 presents the simulation model (§ 2.1) and the results for the radial magnetic field for different expansion times (§§ 2.2 and 2.3). Section 2.4 describes the results for the Parker spiral magnetic field. Finally, § 3 summarizes and discusses the simulation results.
2 Simulation results
2.1 Expanding box model
Here we use the expanding box model (Grappin, Velli & Mangeney Reference Grappin, Velli and Mangeney1993; Grappin & Velli Reference Grappin and Velli1996) implemented to the hybrid code developed by Matthews (Reference Matthews1994) to study the response of a collisionless plasma to a slow expansion. In this hybrid expanding box (HEB) model the expansion is described as an external force; one assumes a solar wind with a constant radial velocity
![]() $v_{sw}$
. Transverse scales (with respect to the radial direction) of a small portion of plasma, co-moving with the solar wind velocity, increase with time as
$v_{sw}$
. Transverse scales (with respect to the radial direction) of a small portion of plasma, co-moving with the solar wind velocity, increase with time as
![]() $1+t/t_{e}$
, where
$1+t/t_{e}$
, where
![]() $t_{e}=R_{0}/v_{sw}$
is the (initial) characteristic expansion time (
$t_{e}=R_{0}/v_{sw}$
is the (initial) characteristic expansion time (
![]() $R_{0}$
being the initial radial distance). The expanding box uses these co-moving coordinates, the physical transverse scales of the simulation box increase with time (see Hellinger & Trávníček Reference Hellinger and Trávníček2005, for a detailed description of the code), and standard periodic boundary conditions are used.
$R_{0}$
being the initial radial distance). The expanding box uses these co-moving coordinates, the physical transverse scales of the simulation box increase with time (see Hellinger & Trávníček Reference Hellinger and Trávníček2005, for a detailed description of the code), and standard periodic boundary conditions are used.
The characteristic spatial and temporal units used in the model are the initial proton inertial length
![]() $d_{p0}=c/\unicode[STIX]{x1D714}_{pp0}$
and the inverse initial proton cyclotron frequency
$d_{p0}=c/\unicode[STIX]{x1D714}_{pp0}$
and the inverse initial proton cyclotron frequency
![]() $1/\unicode[STIX]{x1D714}_{cp0}$
. Here
$1/\unicode[STIX]{x1D714}_{cp0}$
. Here
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $\unicode[STIX]{x1D714}_{pp0}=(n_{p0}e^{2}/m_{p}\unicode[STIX]{x1D716}_{0})^{1/2}$
is the initial proton plasma frequency,
$\unicode[STIX]{x1D714}_{pp0}=(n_{p0}e^{2}/m_{p}\unicode[STIX]{x1D716}_{0})^{1/2}$
is the initial proton plasma frequency,
![]() $\unicode[STIX]{x1D714}_{cp0}=eB_{0}/m_{p}$
,
$\unicode[STIX]{x1D714}_{cp0}=eB_{0}/m_{p}$
,
![]() $B_{0}$
is the initial magnitude of the ambient magnetic field
$B_{0}$
is the initial magnitude of the ambient magnetic field
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
![]() $n_{p0}$
is the initial proton density,
$n_{p0}$
is the initial proton density,
![]() $e$
and
$e$
and
![]() $m_{p}$
are the proton electric charge and mass, respectively; finally,
$m_{p}$
are the proton electric charge and mass, respectively; finally,
![]() $\unicode[STIX]{x1D716}_{0}$
is the dielectric permittivity of vacuum. We use a spatial resolution
$\unicode[STIX]{x1D716}_{0}$
is the dielectric permittivity of vacuum. We use a spatial resolution
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=0.5d_{p0}$
, and there are initially 4096 particles per cell for protons. Fields and moments are defined on a
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=0.5d_{p0}$
, and there are initially 4096 particles per cell for protons. Fields and moments are defined on a
![]() $2048\times 1024$
2D grid (unless stated otherwise). Protons are advanced using the Boris scheme with a time step
$2048\times 1024$
2D grid (unless stated otherwise). Protons are advanced using the Boris scheme with a time step
![]() $\unicode[STIX]{x0394}t=0.05/\unicode[STIX]{x1D714}_{cp0}$
, while the magnetic field
$\unicode[STIX]{x0394}t=0.05/\unicode[STIX]{x1D714}_{cp0}$
, while the magnetic field
![]() $\boldsymbol{B}$
is advanced with a smaller time step
$\boldsymbol{B}$
is advanced with a smaller time step
![]() $\unicode[STIX]{x0394}t_{B}=\unicode[STIX]{x0394}t/10$
. The initial ambient magnetic field is in the 2D simulation box,
$\unicode[STIX]{x0394}t_{B}=\unicode[STIX]{x0394}t/10$
. The initial ambient magnetic field is in the 2D simulation box,
![]() $\boldsymbol{B}_{0}=B_{0}(\cos \unicode[STIX]{x1D703}_{BR},\sin \unicode[STIX]{x1D703}_{BR},0)$
with the initial angle between the magnetic field and the radial direction
$\boldsymbol{B}_{0}=B_{0}(\cos \unicode[STIX]{x1D703}_{BR},\sin \unicode[STIX]{x1D703}_{BR},0)$
with the initial angle between the magnetic field and the radial direction
![]() $\unicode[STIX]{x1D703}_{BR}=0^{\circ }$
and
$\unicode[STIX]{x1D703}_{BR}=0^{\circ }$
and
![]() $32^{\circ }$
. Initially we set
$32^{\circ }$
. Initially we set
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }=2.4$
and
$\unicode[STIX]{x1D6FD}_{p\Vert }=2.4$
and
![]() $T_{p\bot }/T_{p\Vert }=0.7$
to start the simulation close to the unstable region and we set the expansion time
$T_{p\bot }/T_{p\Vert }=0.7$
to start the simulation close to the unstable region and we set the expansion time
![]() $t_{e}=10^{4}/\unicode[STIX]{x1D714}_{cp0}$
(unless stated otherwise).
$t_{e}=10^{4}/\unicode[STIX]{x1D714}_{cp0}$
(unless stated otherwise).
2.2 Radial magnetic field
We start with the well-studied case with the strictly radial magnetic field (Matteini et al.
Reference Matteini, Landi, Hellinger and Velli2006; Hellinger & Trávníček Reference Hellinger and Trávníček2008). In this case the expansion continuously drives
![]() $T_{p\Vert }>T_{p\bot }$
. When no wave activity/turbulence is present, the system is collisionless, and no important heat flux exists one expects that the plasma system follows the double-adiabatic/CGL prediction (Chew et al.
Reference Chew, Goldberger and Low1956) for the parallel and perpendicular proton temperatures
$T_{p\Vert }>T_{p\bot }$
. When no wave activity/turbulence is present, the system is collisionless, and no important heat flux exists one expects that the plasma system follows the double-adiabatic/CGL prediction (Chew et al.
Reference Chew, Goldberger and Low1956) for the parallel and perpendicular proton temperatures
respectively. For the radial magnetic field we have
![]() $B\propto R^{-2}$
and
$B\propto R^{-2}$
and
![]() $n\propto R^{-2}$
, so that
$n\propto R^{-2}$
, so that
![]() $T_{p\Vert }$
is constant and
$T_{p\Vert }$
is constant and
![]() $T_{p\bot }\propto R^{-2}$
.
$T_{p\bot }\propto R^{-2}$
.
Figure 1 displays the evolution in the 2D HEB simulation for the radial magnetic field (
![]() $\unicode[STIX]{x1D703}_{BR}=0^{\circ }$
): the solid curve shows the path in the space
$\unicode[STIX]{x1D703}_{BR}=0^{\circ }$
): the solid curve shows the path in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons with respect to the (blue) parallel and (red) oblique fire hoses; the dotted curve displays the corresponding double-adiabatic/CGL prediction. The system initially follows the CGL prediction
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons with respect to the (blue) parallel and (red) oblique fire hoses; the dotted curve displays the corresponding double-adiabatic/CGL prediction. The system initially follows the CGL prediction
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }\propto R^{2}$
,
$\unicode[STIX]{x1D6FD}_{p\Vert }\propto R^{2}$
,
![]() $T_{p\bot }/T_{p\Vert }\propto R^{-2}$
. When the system enters the region unstable with respect to the parallel fire hose (Gary et al.
Reference Gary, Li, O’Rourke and Winske1998), the generated waves scatter protons and reduce the parallel temperature, which leads to relatively weak departures from the CGL prediction. The system eventually enters the region unstable with respect to the oblique fire hose (Hellinger & Matsumoto Reference Hellinger and Matsumoto2000). The plasma then jumps towards the stable region and after that a CGL-like behaviour reappears and the parallel temperature anisotropy increases. This is stopped by another jump that strongly reduces the theoretical instability growth rates. The oscillations between weakly and strongly unstable regions repeat till the end of the simulations.
$T_{p\bot }/T_{p\Vert }\propto R^{-2}$
. When the system enters the region unstable with respect to the parallel fire hose (Gary et al.
Reference Gary, Li, O’Rourke and Winske1998), the generated waves scatter protons and reduce the parallel temperature, which leads to relatively weak departures from the CGL prediction. The system eventually enters the region unstable with respect to the oblique fire hose (Hellinger & Matsumoto Reference Hellinger and Matsumoto2000). The plasma then jumps towards the stable region and after that a CGL-like behaviour reappears and the parallel temperature anisotropy increases. This is stopped by another jump that strongly reduces the theoretical instability growth rates. The oscillations between weakly and strongly unstable regions repeat till the end of the simulations.

Figure 1. Evolution in 2D HEB simulation for the radial
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the path in the space
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the path in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
is shown by the solid curve; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
is shown by the solid curve; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
![]() $\unicode[STIX]{x1D714}_{cp}$
) as a function of
$\unicode[STIX]{x1D714}_{cp}$
) as a function of
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }$
and
$\unicode[STIX]{x1D6FD}_{p\Vert }$
and
![]() $T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the corresponding double-adiabatic prediction.
$T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the corresponding double-adiabatic prediction.
The oscillatory behaviour is connected with the self-destructive properties of the oblique fire hose. Figure 2 shows the evolution of the fluctuating magnetic energy. Figure 2(a) shows the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. Figure 2(b,c) show colour scale plots of the fluctuating magnetic energy
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. Figure 2(b,c) show colour scale plots of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
![]() $\boldsymbol{k}$
and function of time and angle
$\boldsymbol{k}$
and function of time and angle
![]() $\unicode[STIX]{x1D703}_{kB}$
between the ambient magnetic field and the wave vector, respectively. As the system expands the plasma becomes unstable with respect to the parallel fire hose and relatively weak (
$\unicode[STIX]{x1D703}_{kB}$
between the ambient magnetic field and the wave vector, respectively. As the system expands the plasma becomes unstable with respect to the parallel fire hose and relatively weak (
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}\sim 0.0004$
) quasi-parallel (
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}\sim 0.0004$
) quasi-parallel (
![]() $\unicode[STIX]{x1D703}_{kB}\sim 0^{\circ }$
) propagating modes appear at proton scales (
$\unicode[STIX]{x1D703}_{kB}\sim 0^{\circ }$
) propagating modes appear at proton scales (
![]() $k\sim 0.5d_{p}^{-1}$
) for
$k\sim 0.5d_{p}^{-1}$
) for
![]() $0.10\lesssim t/t_{e}\lesssim 0.15$
. Around
$0.10\lesssim t/t_{e}\lesssim 0.15$
. Around
![]() $t\sim 0.4$
oblique fire hose wave activity appears and mostly disappears quite rapidly (on a time scale
$t\sim 0.4$
oblique fire hose wave activity appears and mostly disappears quite rapidly (on a time scale
![]() ${\sim}0.1t_{e}$
). This self-destructive behaviour is connected with the dispersive properties of the oblique fire hose instability: it destabilizes non-propagating oblique modes that only exist for sufficiently anisotropic protons and, as the generated waves scatter protons and reduce the temperature anisotropy, the non-propagating modes disappear and the fluctuations transform to damped oblique Alfvén waves (Hellinger & Matsumoto Reference Hellinger and Matsumoto2000, Reference Hellinger and Matsumoto2001). The system with a relatively weak level of wave activity then follows a CGL-like evolution leading to the generation of the parallel temperature anisotropy and again (mostly oblique) fire hose activity appears leading to the quasi-periodic oscillations in
${\sim}0.1t_{e}$
). This self-destructive behaviour is connected with the dispersive properties of the oblique fire hose instability: it destabilizes non-propagating oblique modes that only exist for sufficiently anisotropic protons and, as the generated waves scatter protons and reduce the temperature anisotropy, the non-propagating modes disappear and the fluctuations transform to damped oblique Alfvén waves (Hellinger & Matsumoto Reference Hellinger and Matsumoto2000, Reference Hellinger and Matsumoto2001). The system with a relatively weak level of wave activity then follows a CGL-like evolution leading to the generation of the parallel temperature anisotropy and again (mostly oblique) fire hose activity appears leading to the quasi-periodic oscillations in
![]() $\unicode[STIX]{x1D6FF}B$
and in the space
$\unicode[STIX]{x1D6FF}B$
and in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
.
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
.

Figure 2. Evolution in 2D HEB simulation for the radial
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
. (a) Fluctuating magnetic energy
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
. (a) Fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. (b) Colour scale plot of the fluctuating magnetic energy
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. (b) Colour scale plot of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
![]() $\boldsymbol{k}$
. (c) Colour scale plot of the fluctuating magnetic energy
$\boldsymbol{k}$
. (c) Colour scale plot of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and angle
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and angle
![]() $\unicode[STIX]{x1D703}_{kB}$
.
$\unicode[STIX]{x1D703}_{kB}$
.
For the radial magnetic field we recover the previous results (Matteini et al. Reference Matteini, Landi, Hellinger and Velli2006; Hellinger & Trávníček Reference Hellinger and Trávníček2008). The expansion time we used in the HEB simulations is at least 10 times faster than what is typically observed in the solar wind. It is important to investigate the role of the expansion time.
2.3 Role of the expansion time
We performed another simulation with
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
. This value is close to realistic expansion times in the vicinity of 1 a.u. In order to be able to perform a simulation on such much longer time scales compared to the previous case, we reduced the size of the simulation box to
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
. This value is close to realistic expansion times in the vicinity of 1 a.u. In order to be able to perform a simulation on such much longer time scales compared to the previous case, we reduced the size of the simulation box to
![]() $512\times 512$
(while keeping the same resolution and the same initial plasma parameters). We also increased the number of particles per cell to 16 384 to reduce the noise level, so that the corresponding numerical particle scattering is weak on the expansion time scale.
$512\times 512$
(while keeping the same resolution and the same initial plasma parameters). We also increased the number of particles per cell to 16 384 to reduce the noise level, so that the corresponding numerical particle scattering is weak on the expansion time scale.
One expects that for faster expansion the system enters further into the unstable regions and generates stronger wave activity to counteract the expansion-driven anisotropization (Hellinger & Trávníček Reference Hellinger and Trávníček2005; Matteini et al.
Reference Matteini, Landi, Hellinger and Velli2006). Figure 3 shows the evolution in the 2D HEB simulation for the radial magnetic field (
![]() $\unicode[STIX]{x1D703}_{BR}=0^{\circ }$
) and
$\unicode[STIX]{x1D703}_{BR}=0^{\circ }$
) and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
in the same format as in figure 1: the solid curve displays the path in the space
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
in the same format as in figure 1: the solid curve displays the path in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons for (blue) the parallel and (red) the oblique fire hoses. The dotted curve displays the corresponding double-adiabatic/CGL prediction. Figure 3 indeed demonstrates that the system with the slower expansion enters less far into the unstable region. Moreover, this plot suggests that the system does not enter inside the region unstable with respect to the oblique fire hose. On the other hand, the observed oscillations suggest that the oblique fire hose was active.
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons for (blue) the parallel and (red) the oblique fire hoses. The dotted curve displays the corresponding double-adiabatic/CGL prediction. Figure 3 indeed demonstrates that the system with the slower expansion enters less far into the unstable region. Moreover, this plot suggests that the system does not enter inside the region unstable with respect to the oblique fire hose. On the other hand, the observed oscillations suggest that the oblique fire hose was active.

Figure 3. Evolution in 2D HEB simulation for the radial
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
: the path in the space
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
: the path in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
is shown by the solid curve; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
is shown by the solid curve; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
![]() $\unicode[STIX]{x1D714}_{cp}$
) as a function of
$\unicode[STIX]{x1D714}_{cp}$
) as a function of
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }$
and
$\unicode[STIX]{x1D6FD}_{p\Vert }$
and
![]() $T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the corresponding double-adiabatic prediction.
$T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the corresponding double-adiabatic prediction.
Figure 4 shows the evolution of the fluctuating magnetic energy in the same format as in figure 2. Figure 4(a) shows the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. Figure 4(b,c) show colour scale plots of the fluctuating magnetic energy
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. Figure 4(b,c) show colour scale plots of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
![]() $\boldsymbol{k}d_{p}$
and as a function of time and angle
$\boldsymbol{k}d_{p}$
and as a function of time and angle
![]() $\unicode[STIX]{x1D703}_{kB}$
between the ambient magnetic field and the wave vector, respectively.
$\unicode[STIX]{x1D703}_{kB}$
between the ambient magnetic field and the wave vector, respectively.
The evolution is similar to that seen in the simulation with the 10-times faster expansion (see § 2.2). The expansion drives continuously
![]() $T_{p\Vert }>T_{p\bot }$
following the CGL prediction. When the system enters the region unstable to the parallel fire hose, the generated wave activity affects the evolution causing small departures from the CGL prediction. When oblique fire hose activity appears, the system rapidly moves to the less unstable region while a large portion of generated wave activity is damped. After that, the system again evolves in a CGL-like manner and the process repeats quasi-periodically.
$T_{p\Vert }>T_{p\bot }$
following the CGL prediction. When the system enters the region unstable to the parallel fire hose, the generated wave activity affects the evolution causing small departures from the CGL prediction. When oblique fire hose activity appears, the system rapidly moves to the less unstable region while a large portion of generated wave activity is damped. After that, the system again evolves in a CGL-like manner and the process repeats quasi-periodically.
The comparison between the two simulations demonstrates that the evolutions for
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
and
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
are similar (qualitatively and semiquantitatively). The main difference is that the amplitude of fluctuations is smaller for the slower expansion and that the system enters further into the unstable region for the faster expansion. In the case of
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
are similar (qualitatively and semiquantitatively). The main difference is that the amplitude of fluctuations is smaller for the slower expansion and that the system enters further into the unstable region for the faster expansion. In the case of
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
, the bi-Maxwellian linear theory predicts that the system remains stable with respect to the oblique fire hose but in the simulation an important oblique fire hose activity appears. We will look at this phenomenon in detail in the next subsection, in the case of the oblique magnetic field.
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
, the bi-Maxwellian linear theory predicts that the system remains stable with respect to the oblique fire hose but in the simulation an important oblique fire hose activity appears. We will look at this phenomenon in detail in the next subsection, in the case of the oblique magnetic field.

Figure 4. Evolution in 2D HEB simulation with the radial magnetic field and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
. (a) Fluctuating magnetic energy
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{5}$
. (a) Fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. (b) Colour scale plot of the fluctuating magnetic energy
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. (b) Colour scale plot of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
![]() $\boldsymbol{k}$
. (c) Colour scale plot of the fluctuating magnetic energy
$\boldsymbol{k}$
. (c) Colour scale plot of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and angle
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and angle
![]() $\unicode[STIX]{x1D703}_{kB}$
.
$\unicode[STIX]{x1D703}_{kB}$
.
2.4 Oblique magnetic field
The magnetic field in the solar wind is usually oblique with respect to the radial direction. For the expanding box approximation we have from the conservation of the magnetic flux for radial and transverse components of the magnetic field
respectively, in agreement with the ideal Parker spiral model (Parker Reference Parker1958). For a magnetic field close to the radial direction the expansion drives the parallel anisotropy,
![]() $T_{p\Vert }>T_{p\bot }$
, but for a sufficiently oblique magnetic field (
$T_{p\Vert }>T_{p\bot }$
, but for a sufficiently oblique magnetic field (
![]() $\unicode[STIX]{x1D703}_{BR}\gtrsim 45^{\circ }$
) the opposite anisotropy is generated. In this subsection, we investigate this transition starting with
$\unicode[STIX]{x1D703}_{BR}\gtrsim 45^{\circ }$
) the opposite anisotropy is generated. In this subsection, we investigate this transition starting with
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
. This particular value of
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
. This particular value of
![]() $\unicode[STIX]{x1D703}_{BR}$
corresponds to the radial distance
$\unicode[STIX]{x1D703}_{BR}$
corresponds to the radial distance
![]() $R\sim 0.6$
a.u. and was chosen in order to have initially a sufficiently long time of the generation of
$R\sim 0.6$
a.u. and was chosen in order to have initially a sufficiently long time of the generation of
![]() $T_{p\Vert }>T_{p\bot }$
and a relatively long phase where
$T_{p\Vert }>T_{p\bot }$
and a relatively long phase where
![]() $T_{p\Vert }<T_{p\bot }$
is generated at later times of the simulations. The duration of this simulation is
$T_{p\Vert }<T_{p\bot }$
is generated at later times of the simulations. The duration of this simulation is
![]() $t_{max}=2t_{e}$
, so that at the end
$t_{max}=2t_{e}$
, so that at the end
![]() $R\sim 1.8$
a.u. and the ambient magnetic field angle with the radial direction is
$R\sim 1.8$
a.u. and the ambient magnetic field angle with the radial direction is
![]() $\unicode[STIX]{x1D703}_{BR}\sim 62^{\circ }$
.
$\unicode[STIX]{x1D703}_{BR}\sim 62^{\circ }$
.
Figure 5 shows the evolution in the 2D HEB simulation with
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
in the same format as in figures 1 and 3: the solid curve displays the path in the space
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
in the same format as in figures 1 and 3: the solid curve displays the path in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
![]() $\unicode[STIX]{x1D714}_{cp}$
) as a function of
$\unicode[STIX]{x1D714}_{cp}$
) as a function of
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }$
and
$\unicode[STIX]{x1D6FD}_{p\Vert }$
and
![]() $T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the double-adiabatic prediction. The system initially follows the double-adiabatic prediction but when it enters the region unstable with respect to the parallel fire hose this behaviour is slightly affected. The presence of this instability is not sufficient to overcome the temperature anisotropization owing to the expansion in this case. The system enters less far into the unstable region compared to the radial case with the same expansion time (see figure 1) as the anisotropization in the case of the oblique magnetic field is weaker. The plasma does not enter into the region unstable with respect to the oblique fire hose in the corresponding bi-Maxwellian plasma. However, the path in
$T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the double-adiabatic prediction. The system initially follows the double-adiabatic prediction but when it enters the region unstable with respect to the parallel fire hose this behaviour is slightly affected. The presence of this instability is not sufficient to overcome the temperature anisotropization owing to the expansion in this case. The system enters less far into the unstable region compared to the radial case with the same expansion time (see figure 1) as the anisotropization in the case of the oblique magnetic field is weaker. The plasma does not enter into the region unstable with respect to the oblique fire hose in the corresponding bi-Maxwellian plasma. However, the path in
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
exhibits a return movement along almost the same CGL trajectory to the less unstable region, likely due to the destabilization of the oblique fire hose as in the previous subsection. After this, the system follows a double-adiabatic-like path, just shifted in the
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
exhibits a return movement along almost the same CGL trajectory to the less unstable region, likely due to the destabilization of the oblique fire hose as in the previous subsection. After this, the system follows a double-adiabatic-like path, just shifted in the
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
space.
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
space.

Figure 5. Evolution in 2D HEB simulation for
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the path in the space
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the path in the space
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
is shown by the solid curve; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
is shown by the solid curve; the empty circle denotes the initial condition. The dashed contours show the linear prediction in a homogeneous plasma with bi-Maxwellian protons, the maximum growth rate (in units of
![]() $\unicode[STIX]{x1D714}_{cp}$
) as a function of
$\unicode[STIX]{x1D714}_{cp}$
) as a function of
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }$
and
$\unicode[STIX]{x1D6FD}_{p\Vert }$
and
![]() $T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the corresponding double-adiabatic prediction.
$T_{p\bot }/T_{p\Vert }$
for (blue) the parallel proton fire hose and (red) the oblique one. The dotted curve displays the corresponding double-adiabatic prediction.
A more detailed comparison between the simulation results and the double-adiabatic prediction is shown in figure 6 that displays the proton parallel
![]() $T_{p\Vert }$
(a) and perpendicular
$T_{p\Vert }$
(a) and perpendicular
![]() $T_{p\bot }$
(b) as functions of time compared to the prediction. Until about
$T_{p\bot }$
(b) as functions of time compared to the prediction. Until about
![]() $t=0.4t_{e}$
, both the temperatures follow quite closely the double-adiabatic prediction, while around this time there is an important reduction of the parallel temperature and enhancement of the perpendicular one compared to the double-adiabatic prediction. After that, the system follows the double-adiabatic prediction again.
$t=0.4t_{e}$
, both the temperatures follow quite closely the double-adiabatic prediction, while around this time there is an important reduction of the parallel temperature and enhancement of the perpendicular one compared to the double-adiabatic prediction. After that, the system follows the double-adiabatic prediction again.

Figure 6. Evolution in 2D HEB simulation for
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the proton parallel
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the proton parallel
![]() $T_{p\Vert }$
(a) and perpendicular
$T_{p\Vert }$
(a) and perpendicular
![]() $T_{p\bot }$
(b) as functions of time. The dotted curves show the corresponding double-adiabatic predictions.
$T_{p\bot }$
(b) as functions of time. The dotted curves show the corresponding double-adiabatic predictions.
The disruption of the double-adiabatic prediction is caused by the generation of the oblique fire hose fluctuations. Figure 7 shows the evolution of the fluctuating magnetic energy. Figure 7(a) shows the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. Figure 7(b,c) show colour scale plots of the fluctuating magnetic energy
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. Figure 7(b,c) show colour scale plots of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
![]() $\boldsymbol{k}d_{p}$
and as a function of time and angle
$\boldsymbol{k}d_{p}$
and as a function of time and angle
![]() $\unicode[STIX]{x1D703}_{kB}$
between the ambient magnetic field and the wave vector, respectively. As the system expands, the plasma becomes unstable with respect to the parallel fire hose and relatively weak (
$\unicode[STIX]{x1D703}_{kB}$
between the ambient magnetic field and the wave vector, respectively. As the system expands, the plasma becomes unstable with respect to the parallel fire hose and relatively weak (
![]() $\unicode[STIX]{x1D6FF}B/B_{0}\sim 0.01$
) quasi-parallel (
$\unicode[STIX]{x1D6FF}B/B_{0}\sim 0.01$
) quasi-parallel (
![]() $\unicode[STIX]{x1D703}_{kB}\sim 0^{\circ }$
) propagating modes appear at proton scales (
$\unicode[STIX]{x1D703}_{kB}\sim 0^{\circ }$
) propagating modes appear at proton scales (
![]() $k\sim 0.5d_{p}^{-1}$
) for
$k\sim 0.5d_{p}^{-1}$
) for
![]() $0.2\lesssim t/t_{e}\lesssim 0.4$
. Around
$0.2\lesssim t/t_{e}\lesssim 0.4$
. Around
![]() $t\sim 0.4$
, oblique fire hose wave activity appears and mostly disappears quite rapidly (on a time scale
$t\sim 0.4$
, oblique fire hose wave activity appears and mostly disappears quite rapidly (on a time scale
![]() ${\sim}0.1t_{e}$
), similarly to the case with the radial magnetic field.
${\sim}0.1t_{e}$
), similarly to the case with the radial magnetic field.

Figure 7. Evolution in 2D HEB simulation for
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
. (a) Fluctuating magnetic energy
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
. (a) Fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. (b) Colour scale plot of the fluctuating magnetic energy
$\unicode[STIX]{x1D6FF}B^{2}/B_{0}^{2}$
as a function of time. (b) Colour scale plot of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and the wave vector
![]() $\boldsymbol{k}$
. (c) Colour scale plot of the fluctuating magnetic energy
$\boldsymbol{k}$
. (c) Colour scale plot of the fluctuating magnetic energy
![]() $\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and angle
$\unicode[STIX]{x1D6FF}B^{2}$
as a function of time and angle
![]() $\unicode[STIX]{x1D703}_{kB}$
.
$\unicode[STIX]{x1D703}_{kB}$
.
Figure 5 reveals a discrepancy between the linear prediction based on the bi-Maxwellian approximation and the simulation results. As in the case of slower expansion (§ 2.3), the linear theory based on the bi-Maxwellian proton velocity distribution function predicts that the system is all the time stable with respect to the oblique fire hose, whereas the simulation results clearly exhibit a wave activity driven by this instability. This is connected with the resonant character of the instability (Gary Reference Gary1993); its growth rate depends on the details (gradients) of the particle velocity distribution function. Figure 8 shows the maximum growth rate
![]() $\unicode[STIX]{x1D6FE}_{max}$
as a function of time for the parallel (a) and oblique (b) fire hose instabilities. The solid lines display the linear prediction calculated from the distribution function observed in the code (cf. Hellinger & Trávníček Reference Hellinger and Trávníček2011), whereas the dashed line shows the results for bi-Maxwellian velocity distribution functions that have the observed parallel and perpendicular proton temperatures.
$\unicode[STIX]{x1D6FE}_{max}$
as a function of time for the parallel (a) and oblique (b) fire hose instabilities. The solid lines display the linear prediction calculated from the distribution function observed in the code (cf. Hellinger & Trávníček Reference Hellinger and Trávníček2011), whereas the dashed line shows the results for bi-Maxwellian velocity distribution functions that have the observed parallel and perpendicular proton temperatures.

Figure 8. Evolution in 2D HEB simulation for
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the maximum growth rate
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: the maximum growth rate
![]() $\unicode[STIX]{x1D6FE}_{max}$
as a function of time for the parallel (a) and oblique (b) fire hose instabilities. The solid lines display the linear prediction calculated from the proton velocity distribution function, whereas the dashed line shows the results for a bi-Maxwellian velocity distribution function corresponding to the parallel and perpendicular pressures.
$\unicode[STIX]{x1D6FE}_{max}$
as a function of time for the parallel (a) and oblique (b) fire hose instabilities. The solid lines display the linear prediction calculated from the proton velocity distribution function, whereas the dashed line shows the results for a bi-Maxwellian velocity distribution function corresponding to the parallel and perpendicular pressures.
Figure 8 clearly demonstrates that the growth rates calculated from the velocity distribution functions can widely differ from those calculated from bi-Maxwellian distribution functions having the same temperatures (cf. Isenberg Reference Isenberg2012). For the parallel fire hose the two growth rates are the same only initially,
![]() $t\lesssim 0.15t_{e}$
. As the parallel fire hose activity increases, protons are scattered mainly in the resonant region of the velocity distribution function, giving rise to a quasi-linear plateau-like distribution. This plateau does not strongly influence the macroscopic moments, so that the linear prediction based on the bi-Maxwellian shape gives much stronger growth rates. On the other hand, the linear theory based on the instantaneous velocity distribution predicts an important growth rate for the oblique fire hose instability for
$t\lesssim 0.15t_{e}$
. As the parallel fire hose activity increases, protons are scattered mainly in the resonant region of the velocity distribution function, giving rise to a quasi-linear plateau-like distribution. This plateau does not strongly influence the macroscopic moments, so that the linear prediction based on the bi-Maxwellian shape gives much stronger growth rates. On the other hand, the linear theory based on the instantaneous velocity distribution predicts an important growth rate for the oblique fire hose instability for
![]() $0.3t_{e}\lesssim t\lesssim 0.4t_{e}$
, whereas in the corresponding bi-Maxwellian case this mode is stable. This behaviour is caused by the interplay between the expansion and the fire hose instabilities. The expansion affects the whole distribution function, whereas the two fire hose instabilities are resonant and interact preferably with the particles from their resonant regions which are different; the parallel fire hose interacts through the anomalous cyclotron resonance, whereas the oblique fire hose interacts through the cyclotron resonance (and the Landau resonance after the branch change, cf. Hellinger & Trávníček Reference Hellinger and Trávníček2006). As the parallel fire hose is stabilized through the modification of the distribution function in the vicinity of its resonant region, the rest of the distribution function is almost unaffected and may destabilize the oblique fire hose. At the same time, the parallel fire hose reduces the anisotropy on the macroscopic level so that in the corresponding bi-Maxwellian plasma the oblique fire hose is stabilized. The simulation results are in agreement with the linear prediction based on the instantaneous velocity distribution functions; the parallel fire hose activity is saturated around
$0.3t_{e}\lesssim t\lesssim 0.4t_{e}$
, whereas in the corresponding bi-Maxwellian case this mode is stable. This behaviour is caused by the interplay between the expansion and the fire hose instabilities. The expansion affects the whole distribution function, whereas the two fire hose instabilities are resonant and interact preferably with the particles from their resonant regions which are different; the parallel fire hose interacts through the anomalous cyclotron resonance, whereas the oblique fire hose interacts through the cyclotron resonance (and the Landau resonance after the branch change, cf. Hellinger & Trávníček Reference Hellinger and Trávníček2006). As the parallel fire hose is stabilized through the modification of the distribution function in the vicinity of its resonant region, the rest of the distribution function is almost unaffected and may destabilize the oblique fire hose. At the same time, the parallel fire hose reduces the anisotropy on the macroscopic level so that in the corresponding bi-Maxwellian plasma the oblique fire hose is stabilized. The simulation results are in agreement with the linear prediction based on the instantaneous velocity distribution functions; the parallel fire hose activity is saturated around
![]() $t\sim 0.3t_{e}$
, the oblique fire hose wave activity has a maximum amplitude around
$t\sim 0.3t_{e}$
, the oblique fire hose wave activity has a maximum amplitude around
![]() $t\sim 0.4t_{e}$
, and after
$t\sim 0.4t_{e}$
, and after
![]() $t\sim 0.4t_{e}$
all the wave activity decays.
$t\sim 0.4t_{e}$
all the wave activity decays.
The calculation of the linear growth rate is based on discrete velocity distribution functions calculated in the code over the whole simulation box. The distribution function is evaluated on a
![]() $512\times 512$
grid in the velocity space
$512\times 512$
grid in the velocity space
![]() $(v_{\Vert },v_{\bot })$
with respect to the ambient magnetic field. The maximum parallel and perpendicular velocities (and consequently the velocity grid size) are determined in the code by the maximum proton velocities. The finite number of particles per cell and the discretization are sources of different errors. In the present case, we estimate the error of the growth rate determination from the velocity distribution function to be of the order
$(v_{\Vert },v_{\bot })$
with respect to the ambient magnetic field. The maximum parallel and perpendicular velocities (and consequently the velocity grid size) are determined in the code by the maximum proton velocities. The finite number of particles per cell and the discretization are sources of different errors. In the present case, we estimate the error of the growth rate determination from the velocity distribution function to be of the order
![]() $10^{-4}\unicode[STIX]{x1D714}_{cp}$
, so that the values in figure 8 are physically relevant.
$10^{-4}\unicode[STIX]{x1D714}_{cp}$
, so that the values in figure 8 are physically relevant.
The actual shape of the proton velocity distribution function is shown in figure 9, which displays colour scale plots of the distribution functions as functions of
![]() $v_{\bot }$
and
$v_{\bot }$
and
![]() $v_{\Vert }$
(normalized to the Alfvén velocity
$v_{\Vert }$
(normalized to the Alfvén velocity
![]() $v_{A}$
) at (a)
$v_{A}$
) at (a)
![]() $t=0.3t_{e}$
, (b)
$t=0.3t_{e}$
, (b)
![]() $t=0.5t_{e}$
, and (c)
$t=0.5t_{e}$
, and (c)
![]() $t=2t_{e}$
. The dotted contours display the double-adiabatic prediction for comparison (this plot was obtained from the velocity distribution function at
$t=2t_{e}$
. The dotted contours display the double-adiabatic prediction for comparison (this plot was obtained from the velocity distribution function at
![]() $t=0$
and rescaled using Equation (2.1a,b
)). At
$t=0$
and rescaled using Equation (2.1a,b
)). At
![]() $t=0.3t_{e}$
, there are small (hardly discernible) differences between the distribution function and the CGL prediction around
$t=0.3t_{e}$
, there are small (hardly discernible) differences between the distribution function and the CGL prediction around
![]() $|v_{\Vert }|\sim 0.4v_{A}$
. At
$|v_{\Vert }|\sim 0.4v_{A}$
. At
![]() $t=0.5t_{e}$
, when most of the wave activity driven by the two fire hoses is damped, there are clear differences between the distribution function and the CGL prediction. Afterwards, the distribution function essentially only rescales, following the CGL prediction.
$t=0.5t_{e}$
, when most of the wave activity driven by the two fire hoses is damped, there are clear differences between the distribution function and the CGL prediction. Afterwards, the distribution function essentially only rescales, following the CGL prediction.

Figure 9. Evolution in 2D HEB simulation for
![]() $\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
$\unicode[STIX]{x1D703}_{BR}=32^{\circ }$
and
![]() $t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: colour scale plots of the proton velocity distribution functions as functions of
$t_{e}\unicode[STIX]{x1D714}_{cp0}=10^{4}$
: colour scale plots of the proton velocity distribution functions as functions of
![]() $v_{\bot }$
and
$v_{\bot }$
and
![]() $v_{\Vert }$
(normalized to
$v_{\Vert }$
(normalized to
![]() $v_{A}$
) at (a)
$v_{A}$
) at (a)
![]() $t=0.3t_{e}$
, (b)
$t=0.3t_{e}$
, (b)
![]() $t=0.5t_{e}$
, and (c)
$t=0.5t_{e}$
, and (c)
![]() $t=2t_{e}$
. The dotted contours display the double-adiabatic prediction.
$t=2t_{e}$
. The dotted contours display the double-adiabatic prediction.
3 Discussion
We presented three two-dimensional hybrid expanding box simulations of the competition between the expansion-driven parallel proton temperature anisotropy and fire hose instabilities. We used similar plasma parameters and varied the expansion time scale and the (initial) angle between the ambient magnetic field and the radial direction. The simulation results of the three simulations have similar properties; as the expansion drives
![]() $T_{p\Vert }>T_{p\bot }$
, the system becomes unstable with respect the dominant parallel fire hose instability. This instability is generally unable to counteract the induced anisotropization and the system becomes eventually unstable with respect to the oblique fire hose. This instability efficiently reduces the anisotropy and the system becomes stable, while a significant part of the generated electromagnetic fluctuations is damped to protons. As long as the magnetic field is sufficiently close to the radial direction, this evolution repeats itself and the electromagnetic fluctuations accumulate. For a sufficiently oblique magnetic field the expansion drives
$T_{p\Vert }>T_{p\bot }$
, the system becomes unstable with respect the dominant parallel fire hose instability. This instability is generally unable to counteract the induced anisotropization and the system becomes eventually unstable with respect to the oblique fire hose. This instability efficiently reduces the anisotropy and the system becomes stable, while a significant part of the generated electromagnetic fluctuations is damped to protons. As long as the magnetic field is sufficiently close to the radial direction, this evolution repeats itself and the electromagnetic fluctuations accumulate. For a sufficiently oblique magnetic field the expansion drives
![]() $T_{p\bot }>T_{p\Vert }$
and brings the system to the stable region with respect to the fire hose instabilities, where the generated wave activity is damped. This evolution may eventually lead to instabilities driven by
$T_{p\bot }>T_{p\Vert }$
and brings the system to the stable region with respect to the fire hose instabilities, where the generated wave activity is damped. This evolution may eventually lead to instabilities driven by
![]() $T_{p\bot }>T_{p\Vert }$
(Trávníček et al.
Reference Trávníček, Hellinger, Taylor, Escoubet, Dandouras and Lucek2007). For slower driver (longer expansion time) and/or oblique magnetic field, the system enters less far into the unstable region and generates weaker wave amplitudes. Starting with a sufficiently oblique magnetic field, the system may completely avoid the fire hose instabilities. The simulation results also indicate that the assumption of bi-Maxwellian velocity distribution functions may lead to wrong results, as both the fire hoses are resonant and the simulation results show that the linear growth rate is sensitive to the details of the proton distribution function (cf. Hellinger & Trávníček Reference Hellinger and Trávníček2011). We expect similar results for alpha particle driven fire hose instabilities (Maruca et al.
Reference Maruca, Kasper and Gary2012; Verscharen, Bourouaine & Chandran Reference Verscharen, Bourouaine and Chandran2013; Matteini et al.
Reference Matteini, Hellinger, Schwartz and Landi2015). A differential velocity between different ion species is another source of free energy for instabilities (Matteini et al.
Reference Matteini, Hellinger, Goldstein, Landi, Velli and Neugebauer2013). For electromagnetic instabilities the important parameter is the ratio between the differential and Alfvén velocities (Gary Reference Gary1993; Daughton & Gary Reference Daughton and Gary1998). Similar to the case of the parallel temperature anisotropy, the double-adiabatic approximation predicts that this ratio increases with the radial distance for the magnetic field that is not too oblique with respect to the magnetic field (Matteini et al.
Reference Matteini, Hellinger, Landi, Trávníček and Velli2012). For a sufficiently oblique magnetic field this ratio decreases owing to the rotational force (Verscharen et al.
Reference Verscharen, Chandran, Bourouaine and Hollweg2015).
$T_{p\bot }>T_{p\Vert }$
(Trávníček et al.
Reference Trávníček, Hellinger, Taylor, Escoubet, Dandouras and Lucek2007). For slower driver (longer expansion time) and/or oblique magnetic field, the system enters less far into the unstable region and generates weaker wave amplitudes. Starting with a sufficiently oblique magnetic field, the system may completely avoid the fire hose instabilities. The simulation results also indicate that the assumption of bi-Maxwellian velocity distribution functions may lead to wrong results, as both the fire hoses are resonant and the simulation results show that the linear growth rate is sensitive to the details of the proton distribution function (cf. Hellinger & Trávníček Reference Hellinger and Trávníček2011). We expect similar results for alpha particle driven fire hose instabilities (Maruca et al.
Reference Maruca, Kasper and Gary2012; Verscharen, Bourouaine & Chandran Reference Verscharen, Bourouaine and Chandran2013; Matteini et al.
Reference Matteini, Hellinger, Schwartz and Landi2015). A differential velocity between different ion species is another source of free energy for instabilities (Matteini et al.
Reference Matteini, Hellinger, Goldstein, Landi, Velli and Neugebauer2013). For electromagnetic instabilities the important parameter is the ratio between the differential and Alfvén velocities (Gary Reference Gary1993; Daughton & Gary Reference Daughton and Gary1998). Similar to the case of the parallel temperature anisotropy, the double-adiabatic approximation predicts that this ratio increases with the radial distance for the magnetic field that is not too oblique with respect to the magnetic field (Matteini et al.
Reference Matteini, Hellinger, Landi, Trávníček and Velli2012). For a sufficiently oblique magnetic field this ratio decreases owing to the rotational force (Verscharen et al.
Reference Verscharen, Chandran, Bourouaine and Hollweg2015).
The present simulation results are obtained in a collisionless, homogeneous plasma where Coulomb collisions and the presence of an important turbulent solar wind activity (Bruno & Carbone Reference Bruno and Carbone2013) are neglected. We note that a behaviour similar to that presented here was also seen in weakly collisional plasmas (Hellinger & Trávníček Reference Hellinger and Trávníček2015) and simulation results of Hellinger et al. (Reference Hellinger, Matteini, Landi, Verdini, Franci and Trávníček2015) indicate that kinetic instabilities, such as the oblique fire hose, co-exist with fully developed turbulence. Moreover, similar results were also obtained for a completely different driver (velocity shear) of the temperature anisotropy (Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014). Consequently, our results are quite robust and applicable to a wide range of space or astrophysical plasmas.
In the context of the present work, it is interesting to briefly discuss the results of Matteini et al. (Reference Matteini, Landi, Hellinger, Pantellini, Maksimovic, Velli, Goldstein and Marsch2007). The observed change of proton behaviour around 1 a.u. in the
![]() $(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
plane is likely partly connected with the change of the expansion-driven anisotropization around
$(\unicode[STIX]{x1D6FD}_{p\Vert },T_{p\bot }/T_{p\Vert })$
plane is likely partly connected with the change of the expansion-driven anisotropization around
![]() $\unicode[STIX]{x1D703}_{BR}\sim 45^{\circ }$
that corresponds roughly to 1 a.u. However, these observations also indicate that
$\unicode[STIX]{x1D703}_{BR}\sim 45^{\circ }$
that corresponds roughly to 1 a.u. However, these observations also indicate that
![]() $\unicode[STIX]{x1D6FD}_{p\Vert }$
increases with the radial distance even beyond 1 a.u., whereas the double-adiabatic approximation predicts that it should decrease then. This is probably connected with the fact that the solar wind protons do not generally follow the double-adiabatic prediction since they are continuously heated, likely owing to the turbulent cascade. More work is needed to understand the behaviour of turbulence in the expanding solar wind with an oblique magnetic field, the resulting proton energization, and the role of the fire hose instabilities in such a complex system.
$\unicode[STIX]{x1D6FD}_{p\Vert }$
increases with the radial distance even beyond 1 a.u., whereas the double-adiabatic approximation predicts that it should decrease then. This is probably connected with the fact that the solar wind protons do not generally follow the double-adiabatic prediction since they are continuously heated, likely owing to the turbulent cascade. More work is needed to understand the behaviour of turbulence in the expanding solar wind with an oblique magnetic field, the resulting proton energization, and the role of the fire hose instabilities in such a complex system.
Acknowledgements
The author acknowledges grant 15-10057S of the Grant Agency of the Czech Republic and projects RVO:67985815 and RVO:68378289.