Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-13T11:01:14.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Shearless bifurcations in particle transport for reversed-shear tokamaks

Part of: Hamiltonian Methods in Plasma Physics

Published online by Cambridge University Press:  15 February 2023

G.C. Grime Open the ORCID record for G.C. Grime [Opens in a new window] ,
M. Roberto ,
R.L. Viana Open the ORCID record for R.L. Viana [Opens in a new window] ,
Y. Elskens Open the ORCID record for Y. Elskens [Opens in a new window]  and
I.L. Caldas
G.C. Grime
Affiliation:
Institute of Physics, University of São Paulo, São Paulo, SP 05508-090, Brazil
M. Roberto
Affiliation:
Physics Department, Aeronautics Institute of Technology, São José dos Campos, SP 1228-900, Brazil
R.L. Viana*
Affiliation:
Institute of Physics, University of São Paulo, São Paulo, SP 05508-090, Brazil Physics Department, Federal University of Paraná, Curitiba, PR 81531-990, Brazil
Y. Elskens
Affiliation:
Aix-Marseille University, UMR 7345 CNRS, PIIM, Campus Saint-Jérôme, Case 322, av. esc. Normandie-Niemen 52, FR-13397 Marseille CEDEX 13, France
I.L. Caldas
Affiliation:
Institute of Physics, University of São Paulo, São Paulo, SP 05508-090, Brazil
*
†Email address for correspondence: viana@fisica.ufpr.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Some internal transport barriers in tokamaks have been related to the vicinity of extrema of the plasma equilibrium profiles. This effect is numerically investigated by considering the guiding-centre trajectories of plasma particles undergoing $\boldsymbol {E}\times \boldsymbol {B}$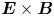 drift motion, considering that the electric field has a stationary non-monotonic radial profile and an electrostatic fluctuation. In addition, the equilibrium configuration has a non-monotonic safety factor profile. The numerical integration of the equations of motion yields a symplectic map with shearless barriers. By changing the safety factor profile parameters, the appearance and breakup of these shearless curves are observed. The shearless curve's successive breakup and recovery are explained using concepts from bifurcation theory. We also present bifurcation sequences associated with the creation of multiple shearless curves. Physical consequences of scenarios with multiple shearless curves are discussed.

Keywords

fusion plasmaplasma nonlinear phenomenaplasma dynamics
Type
Research Article
Information
Journal of Plasma Physics , Volume 89 , Issue 1 , February 2023 , 835890101
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Caldas, I.L., Viana, R.L., Abud, C.V., Fonseca, J.C.D., Guimarães Filho, Z.O., Kroetz, T., Marcus, F.A., Schelin, A.B., Szezech, J.D. Jr. & Toufen, D.L. 2012 Shearless transport barriers in magnetically confined plasmas. Plasma Phys. Control. Fusion 54, 124035.CrossRefGoogle Scholar
del-Castillo-Negrete, D. 2000 Chaotic transport in zonal flows in analogous geophysical and plasma systems. Phys. Plasmas 7, 1702.CrossRefGoogle Scholar
del-Castillo-Negrete, D., Greene, J.M. & Morrison, P.J. 1996 Area preserving nontwist maps: periodic orbits and transition to chaos. Physica D 91, 1.CrossRefGoogle Scholar
Connor, J.W., Fukuda, T., Garbet, X., Gormezano, C., Mukhovatov, V. & Wakatani, M. 2004 A review of internal transport barrier physics for steady-state operation of tokamaks. Nucl. Fusion 44, R1.Google Scholar
Connor, J.W. & Taylor, J.B. 1987 Ballooning modes or Fourier modes in a toroidal plasma? Phys. Fluids 30, 3180.CrossRefGoogle Scholar
Diamond, P.H., Itoh, S.-I. & Itoh, K. 2010 Modern Plasma Physics. Cambridge University Press.CrossRefGoogle Scholar
El Mouden, M., Saifaoui, D., Zine, B. & Eddahoy, M. 2007 Transport barriers with magnetic shear in a tokamak. J. Plasma Phys. 73, 439.CrossRefGoogle Scholar
Falessi, M.V., Pegoraro, F. & Schep, T.J. 2015 Lagrangian coherent structures and plasma transport processes. J. Plasma Phys. 81, 495810505.CrossRefGoogle Scholar
Gentle, K.W., Liao, K., Lee, K. & Rowan, W.L. 2010 Comparison of velocity shear with turbulence reduction driven by biasing in a simple cylindrical slab plasma. Plasma Sci. Technol. 12, 391.CrossRefGoogle Scholar
Goldston, R.J. 1984 Energy confinement scaling in Tokamaks: some implications of recent experiments with Ohmic and strong auxiliary heating. Plasma Phys. Control. Fusion 26, 87.CrossRefGoogle Scholar
Hazeltine, R.D. & Meiss, J.D. 2003 Plasma Confinement. Dover.Google Scholar
Horton, W. 2018 Turbulent Transport in Magnetized Plasmas. World Scientific.Google Scholar
Horton, W. & Benkadda, S. 2015 ITER Physics. World Scientific.Google Scholar
Horton, W., Park, H.B., Kwon, J.M., Strozzi, D., Morrison, P.J. & Choi, D.I. 1998 Drift wave test particle transport in reversed shear profile. Phys. Plasmas 5, 3910.CrossRefGoogle Scholar
Joffrin, E. 2007 Advanced tokamak scenario developments for the next step. Plasma Phys. Control. Fusion 49, B629.CrossRefGoogle Scholar
Joffrin, E., Challis, C.D., Conway, G.D., Garbet, X., Gude, A., Günter, S., Hawkes, N.C., Hender, T.C., Howell, D.F. & Huysmans, G.T.A. 2003 Internal transport barrier triggering by rational magnetic flux surfaces in tokamaks. Nucl. Fusion 43, 1167.CrossRefGoogle Scholar
Kerner, W. & Tasso, H. 1982 Tearing mode stability for arbitrary current distribution. Plasma Phys. 24, 97.CrossRefGoogle Scholar
Kwon, J.-M., Horton, W., Zhu, P., Morrison, P.J., Park, H.-B. & Choi, D.I. 2000 Global drift wave map test particle simulations. Phys. Plasmas 7, 1169.Google Scholar
Lichtenberg, A.J. & Lieberman, M.A. 1997 Regular and Chaotic Motion, 2nd edn. Springer.Google Scholar
MacKay, R.S., Meiss, J.D. & Percival, I.C. 1984 Transport in Hamiltonian systems. Physica D 13, 55.CrossRefGoogle Scholar
Marcus, F.A., Caldas, I.L., Guimarães Filho, Z.O., Morrison, P.J., Horton, W., Kuznetsov, Y.K. & Nascimento, I.C. 2008 Reduction of chaotic particle transport driven by drift waves in sheared flows. Phys. Plasmas 15, 112304.CrossRefGoogle Scholar
Marcus, F.A., Roberto, M., Caldas, I.L., Rosalem, K.C. & Elskens, Y. 2019 Influence of the radial electric field on the shearless transport barriers in tokamaks. Phys. Plasmas 26, 022302.CrossRefGoogle Scholar
Mazzucato, E., Batha, S.H., Beer, M., Bell, M., Bell, R.E., Budny, R.V., Bush, C., Hahm, T.S., Hammett, G.W. & Levinton, F.M. 1996 Turbulent fluctuations in TFTR configurations with reversed magnetic shear. Phys. Rev. Lett. 77, 3145.CrossRefGoogle ScholarPubMed
Morrison, P.J. 2000 Magnetic field lines, Hamiltonian dynamics, and nontwist systems. Phys. Plasmas 7, 2279.CrossRefGoogle Scholar
Nascimento, I.C., Kuznetsov, Y.K., Severo, J.H.F., Fonseca, A.M.M., Elfimov, A., Bellintani, V., Machida, M., Heller, M.V.A.P., Galvão, R.M.O. & Sanada, E.K. 2005 Plasma confinement using biased electrode in the TCABR tokamak. Nucl. Fusion 45, 796.CrossRefGoogle Scholar
Osorio, L., Roberto, M., Caldas, I.L., Viana, R.L. & Elskens, Y. 2021 Onset of internal transport barriers in tokamaks. Phys. Plasmas 28, 082305.CrossRefGoogle Scholar
Rosalem, K.C., Roberto, M. & Caldas, I.L. 2014 Influence of the electric and magnetic shears on tokamak transport. Nucl. Fusion 54, 064001.CrossRefGoogle Scholar
Rosalem, K.C., Roberto, M. & Caldas, I.L. 2016 Drift-wave transport in the velocity shear layer. Phys. Plasmas 23, 072504.CrossRefGoogle Scholar
Sips, A.C.C., et al. 2005 Advanced scenarios for ITER operation. Plasma Phys. Control. Fusion 47, A19.CrossRefGoogle Scholar
Szezech, J.D., Caldas, I.L., Lopes, S.R., Morrison, P.J. & Viana, R.L. 2012 Effective transport barriers in nontwist systems. Phys. Rev. E 86, 036206.CrossRefGoogle ScholarPubMed
Szezech, J.D. Jr, Caldas, I.L., Lopes, S.R., Viana, R.L. & Morrison, P.J. 2009 Transport properties in nontwist area-preserving maps. Chaos 19, 043108.CrossRefGoogle ScholarPubMed
Toufen, D.L., Guimarães Filho, Z.O., Caldas, I.L., Marcus, F.A. & Gentle, K.W. 2012 Turbulence driven particle transport in Texas Helimak. Phys. Plasmas 19, 012307.CrossRefGoogle Scholar
Viezzer, E., Pütterich, T., Conway, G.D. , Dux, R. , Happel, T., Fuchs, J.C., McDermott, R.M., Ryter, F., Sieglin, B. & Suttrop, W. 2013 High-accuracy characterization of the edge radial electric field at ASDEX Upgrade. Nucl. Fusion 53, 053005.CrossRefGoogle Scholar
Wagner, F., Becker, G., Behringer, K., Campbell, D., Eberhagen, A., Engelhardt, W., Fussmann, G., Gehre, O., Gernhardt, J. & Gierke, G.V. 1982 Regime of improved confinement and high beta in neutral-beam-heated divertor discharges of the ASDEX tokamak. Phys. Rev. Lett. 49, 1408.CrossRefGoogle Scholar
White, R.B. 2012 Modification of particle distributions by MHD instabilities I. Commun Nonlinear Sci. Numer. Simul. 17, 2200.CrossRefGoogle Scholar
White, R.B. & Chance, M.S. 1984 Hamiltonian guiding center drift orbit calculation for plasmas of arbitrary cross section. Phys. Fluids 27, 2455.CrossRefGoogle Scholar
Wolf, R.C. 2002 Internal transport barriers in tokamak plasmas. Plasma Phys. Control. Fusion 45, R1.CrossRefGoogle Scholar
Wurm, A., Apte, A., Fuchss, K. & Morrison, P.J. 2005 Meanders and reconnection–collision sequences in the standard nontwist map. Chaos 15, 023108.CrossRefGoogle ScholarPubMed
Wurm, A. & Martini, K.M. 2013 Breakup of inverse golden mean shearless tori in the two-frequency standard nontwist map. Phys. Lett. A 377, 622.CrossRefGoogle Scholar
Yushmanov, P.N., Takizuka, T., Riedel, K.S., Kardaun, O.J.W.F., Cordey, J.G., Kaye, S.M. & Post, D.E. 1990 Scalings for tokamak energy confinement. Nucl. Fusion 30, 1999.CrossRefGoogle Scholar
Zimbardo, G., Pommois, P. & Veltri, P. 2000 The Kubo number as a parameter governing the level of chaos in magnetic turbulence. Physica A 280, 99.CrossRefGoogle Scholar