Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T02:55:19.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple, general, realistic, robust, analytic tokamak equilibria. Part 2. Pedestals and flow

Part of: Focus on Fusion

Published online by Cambridge University Press:  14 May 2021

L. Guazzotto Open the ORCID record for L. Guazzotto [Opens in a new window]  and
J. P. Freidberg Open the ORCID record for J. P. Freidberg [Opens in a new window]
L. Guazzotto
Affiliation:
Physics Department, Auburn University, Auburn, AL36849, USA
J. P. Freidberg*
Affiliation:
MIT, Plasma Science and Fusion Center, Cambridge, MA02139, USA
*
† Email address for correspondence: jpfreid@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Part 1 described a wide range of analytic tokamak equilibria modelling smooth limiter surfaces, double- and single-null divertor surfaces, arbitrary aspect ratio, elongation, triangularity and beta. Part 2 generalizes the analysis to further include edge pedestals and toroidal flow. Specifically, edge pedestals are allowed in the pressure, pressure gradient and toroidal current density. Also, an edge-localized contribution to the bootstrap current is treated. In terms of flow, analytic solutions are obtained for two cases: a 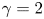$\gamma = 2$ adiabatic and a 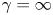$\gamma = \infty $ incompressible energy conservation relation.

Keywords

fusion plasmaplasma confinementplasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 3 , June 2021 , 905870305
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belien, A. J. C., Botchev, M. A., Goedbloed, J. P., Van der Holst, B. & Keppens, R. 2002 FINESSE: axisymmetric MHD equilibria with flow. J. Comput. Phys. 182, 91.CrossRefGoogle Scholar
Cerfon, A. & Freidberg, J. P. 2010 “One size fits all” analytic solutions to the Grad–Shafranov equation. Phys. Plasmas 17, 032502.CrossRefGoogle Scholar
Clemente, R. A. & Farengo, R. 1984 A class of rotating compact tori equilibria. Phys. Fluids 27, 776.CrossRefGoogle Scholar
Del Zanna, L. & Chiuderi, C. 1996 Exact solutions for symmetric magnetohydrodynamic equilibria with mass flow. Astron. Astrophys. 310, 341.Google Scholar
D'Ippolito, D. A., Freidberg, J. P., Goedbloed, J. P. & Rem, J. 1978 High-beta tokamaks surrounded by force-free fields. Phys. Fluids 21, 1600.CrossRefGoogle Scholar
Freidberg, J. P. 1985 Ideal Magnetohydrodynamics, pp. 162–167. Plenum.Google Scholar
Freidberg, J. P. & Grossmann, W. 1975 Magnetohydrodynamic stability of a sharp boundary model of tokamak. Phys. Fluids 18, 1494.CrossRefGoogle Scholar
Guazzotto, L., Betti, R., Manickam, J. & Kaye, S. 2004 Numerical study of tokamak equilibria with arbitrary flow. Phys. Plasmas 11, 604.CrossRefGoogle Scholar
Hameiri, E. 1983 The equilibrium and stability of rotating plasmas. Phys. Fluids 26, 230.CrossRefGoogle Scholar
Haverkort, J., de Blank, H. & Koren, B. 2012 The Brunt–Väisälä frequency of rotating tokamak plasmas. J. Comput. Phys. 231, 981.CrossRefGoogle Scholar
Helander, P. & Sigmar, D. J. 2002 Collisional Transport in Magnetized Plasmas, p. 207. Cambridge University Press.Google Scholar
Iacono, R., Bondeson, A., Troyon, F. & Gruber, R. 1990 Axisymmetric toroidal equilibrium with flow and anisotropic pressure. Phys. Fluids B2, 1794.CrossRefGoogle Scholar
Kaltsas, D. A., Kuiroukidis, A. & Throumoulopoulos, G. N. 2019 A tokamak pertinent analytic equilibrium with plasma flow of arbitrary direction. Phys. Plasmas 26, 124501.CrossRefGoogle Scholar
Kuiroukidis, A. & Throumoulopoulos, G. N. 2014 An analytic nonlinear toroidal equilibrium with flow. Plasma Phys. Control. Fusion 56, 075003.CrossRefGoogle Scholar
Maschke, E. K. & Perrin, H. 1980 Exact analytic solution of the stationary MHD equilibrium equation of a toroidal plasma in rotation. Plasma Phys. 22, 579.CrossRefGoogle Scholar
Miller, R. L., Chu, M. S., Greene, J. M., Lin-Liu, Y. R. & Waltz, R. E. 1998 Noncircular, finite aspect ratio, local equilibrium model. Phys. Plasmas 5, 973.CrossRefGoogle Scholar
Morozov, A. I. & Solov'ev, L. S. 1980 Steady-state plasma flow in a magnetic field. Rev. Plasma Phys. 8, 1.Google Scholar
Semenzato, S., Gruber, R. & Zehrfeld, H. P. 1984 Computation of symmetric ideal MHD flow equilibria. Comput. Phys. Rep. 1, 398.CrossRefGoogle Scholar
Shi, B. 2005 Analytic description of high poloidal beta equilibrium with a natural inboard poloidal field null. Phys. Plasmas 12, 122504.CrossRefGoogle Scholar
Solov'ev, L. S. 1968 The theory of hydromagnetic stability of toroidal plasma configurations. Sov. Phys. JETP 26, 400.Google Scholar
Throumoulopoulos, G. N. & Pantis, G. 1989 Analytic axisymmetric magnetohydrodynamic equilibria of a plasma torus with toroidal mass flow. Phys. Fluids B 1, 1827.CrossRefGoogle Scholar
Todd, A. M. M., Manickam, J., Okabayashi, M., Chance, M. S., Grimm, R. C., Greene, J. M. & Johnson, J. L. 1979 Dependence of ideal-MHD kink and ballooning modes on plasma shape and profiles in tokamaks. Nucl. Fusion 19, 743.CrossRefGoogle Scholar
Tsui, K. H., Navia, C. E., Serbeto, A. & Shigueoka, H. 2011 Tokamak equilibria with non field-aligned axisymmetric divergence-free rotational flows. Phys. Plasmas 18, 072502.CrossRefGoogle Scholar
Weening, R. H. 2000 Analytic spherical torus plasma equilibrium model. Phys. Plasmas 7, 3654.CrossRefGoogle Scholar
Zehrfeld, H. P. & Green, B. J. 1972 Stationary toroidal equilibria at finite beta. Nucl. Fusion 12, 569.CrossRefGoogle Scholar
Zheng, S. B., Wootton, A. J. & Solano, E. R. 1996 Analytical tokamak equilibrium for shaped plasmas. Phys. Plasmas 3, 1176.CrossRefGoogle Scholar