Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T03:38:50.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of the Bernstein modes for large values of the plasma parameter

Published online by Cambridge University Press:  13 March 2009

R. W. Fredricks
R. W. Fredricks
Affiliation:
Space Sciences Laboratory, TRW Systems Group, One Space Park, Redondo Beach, California 90278
Get access Rights & Permissions [Opens in a new window]

Abstract

The electrostatic modes for which k is perpendicular to the impressed field B0 (the ‘Bernstein modes’) have been examined, and dispersion curves (w vs. k) have been calculated numerically for hybrid frequencies in the vicinity of the thirtieth to fortieth harmonic of the gyrofrequency. 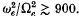Although the calculations were performed for the lower hybrid case (ion branch), they also apply to the upper hybrid cases in which the plasma parameter The structure of the dispersion curves for these large values of plasma parameter differs from that for smaller values 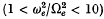investigated by others, in that broad bands in wave-number space have very small group speeds in narrow frequency bands close to many of the gyrofrequency harmonics. All of the Bernstein modes examined have group speeds less than 37 % of the ion thermal speed, and can be classified as very slow waves. Furthermore, the spectrum of propagating Bernstein modes is broadened as 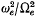becomes large, with an effective total transmission region from the gyrofrequency up to several harmonics of gyrofrequency above the hybrid frequency.

Type
Research Article
Information
Journal of Plasma Physics , Volume 2 , Issue 2 , June 1968 , pp. 197 - 206
Copyright
Copyright © Cambridge University Press 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aamodt, R. E. 1967 Plasma Phys. 9, 573.CrossRefGoogle Scholar
Bernstein, I. B. 1958 Phys. Rev. 109, 10.CrossRefGoogle Scholar
Calvert, W. & Goe, G. B. 1963 J. Geophys. Res. 68, 6113.CrossRefGoogle Scholar
Crawford, F. W. 1965 Radio science, 69.Google Scholar
Crawford, F. W., Harp, R. S. & Mantei, T. D. 1967 J. Geophys. Res. 72, 57.CrossRefGoogle Scholar
Crawford, F. W., Kino, G. & Weiss, H. 1964 a Stanford University Microwave Laboratory Rep. no. 1210. Stanford, California, U.S.A.Google Scholar
Crawford, F. W., Kino, G. & Weiss, H. 1964b Phys. Rev. Letters 13, 229.CrossRefGoogle Scholar
Crawford, F. W. & Weiss, H. 1966 J. Nucl. Energy, pt. C, 8, 21.CrossRefGoogle Scholar
Dougherty, J. P. & Monaghan, J. J. 1966 Proc. Roy. Soc. Lond. A 289, 214.Google Scholar
Fejer, J. A. & Calvert, W. 1964 J. Geophys. Res. 69, 5049.CrossRefGoogle Scholar
Gross, E. P. 1951 Phys. Rev. 82, 232.CrossRefGoogle Scholar
Harp, R. S. 1965 Appl. Phys. Letters 6, 51.CrossRefGoogle Scholar
Nuttall, J. 1964 RCA Victor Research Rep. 7-801-29c. Montreal, Canada.Google Scholar
Shkarofsky, I. P. 1966a Phys. Fluids 9, 561.CrossRefGoogle Scholar
Shkarofsky, I. P. 1966b Phys. Fluids 9, 570.CrossRefGoogle Scholar
Stix, T. H. 1962 Theory of Plasma Waves. New York: McGraw-Hill Book Company.Google Scholar
Sturrock, P. A. 1965 Phys. Fluids 8, 88.CrossRefGoogle Scholar