Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T17:53:37.945Z Has data issue: false hasContentIssue false
  • English
  • Français

Suppression of turbulence in the drift-resistive plasma where zonal flow changes direction

Part of: Focus on Fusion

Published online by Cambridge University Press:  11 June 2020

Chang-Bae Kim Open the ORCID record for Chang-Bae Kim [Opens in a new window]
Chang-Bae Kim*
Affiliation:
Physics Department and Research Institute for Origin of Matter and Evolution of Galaxies, Soongsil University, Seoul06978, Korea
*
†Email address for correspondence: cbkim@ssu.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

The edge region of quasi-adiabatic plasma is pedagogically simulated by the dynamics between the electric potential 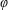$\unicode[STIX]{x1D711}$ and the electron density $n$ whose equilibrium density gradient is negative and held fixed. The zonal flow (ZF) 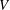$V$ is either enforced sinusoidally or generated self-consistently from the turbulence. Cross-phase 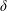$\unicode[STIX]{x1D6FF}$ between 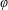$\unicode[STIX]{x1D711}$ and $n$, which is important in the determination of the turbulence level and the transport, is strongly influenced by the ZF. In the region near 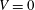$V=0$, 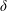$\unicode[STIX]{x1D6FF}$ becomes negative due to the large gradient of the ZF. It is found that the instabilities are quenched there, and the fluctuations decay. The ZF thus works as a transport barrier in the region where the ZF changes direction with large gradient.

Keywords

fusion plasmaplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 3 , June 2020 , 905860315
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakawa, A. 1966 Computational design for long-term numerical integrations of the equations of atmospheric motion. J. Comput. Phys. 1, 110.CrossRefGoogle Scholar
Biglari, H., Diamond, P. H. & Terry, P. W. 1990 Influence of sheared poloidal rotation on edge turbulence. Phys. Fluids B 2, 1.CrossRefGoogle Scholar
Birkenmeier, G., Ramisch, M., Schmid, B. & Stroth, U. 2013 Experimental evidence of turbulent transport regulation by zonal flows. Phys. Rev. Lett. 110, 145004.CrossRefGoogle ScholarPubMed
Burrell, K. H. 1999 Tests of causality: experimental evidence that sheared $\boldsymbol{E}\times \boldsymbol{B}$ flow alters turbulence and transport in tokamaks. Phys. Plasmas 6, 4418.CrossRefGoogle Scholar
Carmargo, S. J., Tippett, M. K. & Caldas, I. L. 1998 Nonmodal energetics of resistive drift waves. Phys. Rev. E 58, 3693.Google Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Hahm, T. S. 2005 Zonal flows in plasma – a review. Plasma Phys. Control. Fusion 47, R35.CrossRefGoogle Scholar
Dudson, B. D., Umansky, M. V., Xu, X. Q., Snyder, P. B. & Wilson, H. R. 2009 Bout$++$: a framework for parallel plasma fluid simulations. Comput. Phys. Commun. 180, 1467.CrossRefGoogle Scholar
Figarella, C. F., Benkadda, S., Beyer, P., Garbet, X. & Voitsekhovitch, I. 2003 Transport reduction by rotation shear in tokamak-edge turbulence. Phys. Rev. Lett. 90, 015002.CrossRefGoogle ScholarPubMed
Freethy, S. J., Görler, T., Creely, A. J., Conway, G. D., Denk, S. S., Happel, T., Koenen, C., Hennequin, P., White, A. E.& ASDEX Upgrade Team 2018 Validation of gyrokinetic simulations with measurements of electron temperature fluctuations and density–temperature phase angles on ASDEX upgrade. Phys. Plasmas 25, 055903.CrossRefGoogle Scholar
Fujisawa, A. 2009 A review of zonal flow experiments. Nucl. Fusion 49, 013001.CrossRefGoogle Scholar
Guttenfelder, W., Kaye, S. M., Kriete, D. M., Bell, R. E., Diallo, A., LeBlanc, B. P., McKee, G. R., Podesta, M., Sabbagh, S. A. & Smith, D. R. 2019 Initial transport and turbulence analysis and gyrokinetic simulation validation in NSTX-U L-mode plasmas. Nucl. Fusion 59, 056027.CrossRefGoogle Scholar
Hasegawa, A. & Wakatani, M. 1983 Plasma edge turbulence. Phys. Rev. Lett. 50, 682.CrossRefGoogle Scholar
Hillesheim, J. C., Delabie, E., Meyer, H., Maggi, C. F., Meneses, L., Poli, E.& JET Contributors 2016 Stationary zonal flows during the formation of the edge transport barrier in the jet tokamak. Phys. Rev. Lett. 116, 065002.CrossRefGoogle ScholarPubMed
Horton, W. 1999 Drift waves and transport. Rev. Mod. Phys. 71, 735.CrossRefGoogle Scholar
Kim, C.-B., An, C.-Y. & Min, B. 2019a Reduction of edge plasma turbulence via cross-phase decrease by zonal fields. Plasma Phys. Control. Fusion 61 (8), 085024.CrossRefGoogle Scholar
Kim, C.-B., Min, B. & An, C.-Y. 2018 Localization of the eigenmode of the drift-resistive plasma by zonal flow. Phys. Plasmas 25 (10), 102501.CrossRefGoogle Scholar
Kim, C.-B., Min, B. & An, C.-Y. 2019b On the effects of nonuniform zonal flow in the resistive-drift plasma. Plasma Phys. Control. Fusion 61 (3), 035002.CrossRefGoogle Scholar
Kobayashi, T., Itoh, K., Ido, T., Kamiya, K., Itoh, S.-I., Miura, Y., Nagashima, Y., Fujisawa, A., Inagaki, S. & Ida, K. 2017 Turbulent transport reduction induced by transition on radial electric field shear and curvature through amplitude and cross-phase in torus plasma. Sci. Rep. 7, 14971.CrossRefGoogle ScholarPubMed
Krommes, J. A. & Kim, C.-B. 2000 Interactions of disparate scales in drift-wave turbulence. Phys. Rev. E 62, 8508.Google ScholarPubMed
Makwana, K. D., Terry, P. W., Pueschel, M. J. & Hatch, D. R. 2014 Subdominant modes in zonal-flow-regulated turbulence. Phys. Rev. Lett. 112, 095002.CrossRefGoogle ScholarPubMed
Naulin, V. & Spatschek, K. H. 1997 Nonlinear drift-wave structures and their influence on particle transport. Phys. Rev. E 55, 5883.Google Scholar
Numata, R., Ball, R. & Dewar, R. L. 2007 Bifurcation in electrostatic resistive drift wave turbulence. Phys. Plasmas 14, 102312.CrossRefGoogle Scholar
Rosenbluth, M. N. & Hinton, F. L. 1998 Poloidal flow driven by ion-temperature-gradient turbulence in tokamaks. Phys. Rev. Lett. 80, 724.CrossRefGoogle Scholar
Schaffner, D. A., Carter, T. A., Rossi, G. D., Guice, D. S., Maggs, J. E., Vincena, S. & Friedman, B. 2012 Modification of turbulent transport with continuous variation of flow shear in the large plasma device. Phys. Rev. Lett. 109, 135002.CrossRefGoogle ScholarPubMed
Shaing, K. C. & Crume, E. C. 1989 Bifurcation theory of poloidal rotation in tokamaks: a model for L–H transition. Phys. Rev. Lett. 63, 2369.CrossRefGoogle Scholar
Shchepetov, S. V., Kholnov, Yu. V. & Vasil’kov, D. G. 2013 On the phase shift between electric potential and plasma density fluctuations in the edge turbulence. Plasma Phys. Rep. 39, 130.CrossRefGoogle Scholar
Terry, P. W. 2000 Suppression of turbulence and transport by sheared flow. Rev. Mod. Phys. 72, 109.CrossRefGoogle Scholar
Terry, P. W., Newman, D. E. & Ware, A. S. 2001 Suppression of transport cross phase by strongly sheared flow. Phys. Rev. Lett. 87, 185001.CrossRefGoogle Scholar
Tynan, G. R., Fujisawa, A. & McKee, G. 2009 A review of experimental drift turbulence studies. Plasma Phys. Control. Fusion 51, 113001.CrossRefGoogle Scholar
Wagner, F. 2018 The history of research into improved confinement. Eur. Phys. J. H 43, 523.Google Scholar
Wagner, F., Becker, G., Behringer, K., Campbell, D., Eberhagen, A., Engelhardt, W., Fussmann, G., Gehre, O., Gernhardt, J., Gierke, G. v. et al. 1982 Regime of improved confinement and high beta in neutral-beam-heated divertor discharges of the ASDEX tokamak. Phys. Rev. Lett. 49, 1408.CrossRefGoogle Scholar
White, A. E., Peebles, W. A., Rhodes, T. L., Holland, C. H., Wang, G., Schmitz, L., Carter, T. A., Hillesheim, J. C., Doyle, E. J., Zeng, L. et al. 2010 Measurement of the cross-phase angle between density and electron temperature fluctuations and comparison with gyrokinetic simulations. Phys. Plasmas 17, 056103.CrossRefGoogle Scholar