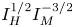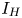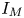1 Introduction
In recent years, there has been significant interest in the study of decaying turbulent magnetic fields. One of the main applications has been to the understanding of the magnetic field evolution during the radiation-dominated era of the early universe (Brandenburg, Enqvist & Olesen Reference Brandenburg, Enqvist and Olesen1996; Christensson, Hindmarsh & Brandenburg Reference Christensson, Hindmarsh and Brandenburg2001; Banerjee & Jedamzik Reference Banerjee and Jedamzik2004). The special case with finite magnetic helicity has been studied and understood for a long time (Hatori Reference Hatori1984; Biskamp & Müller Reference Biskamp and Müller1999). It is the prime example of large-scale magnetic field growth due to an inverse cascade. The possibility of such an inverse cascade is explained by the conservation of magnetic helicity (Frisch et al. Reference Frisch, Pouquet, Leorat and Mazure1975). However, even in the absence of magnetic helicity, an inverse cascade can develop (Kahniashvili et al. Reference Kahniashvili, Tevzadze, Brandenburg and Neronov2013; Zrake Reference Zrake2014; Brandenburg, Kahniashvili & Tevzadze Reference Brandenburg, Kahniashvili and Tevzadze2015), and it is well explained by the conservation of what is now called the Hosking integral (Hosking & Schekochihin Reference Hosking and Schekochihin2021, Reference Hosking and Schekochihin2023a; Zhou, Sharma & Brandenburg Reference Zhou, Sharma and Brandenburg2022; Brandenburg, Sharma & Vachaspati Reference Brandenburg, Sharma and Vachaspati2023c), which is the correlation integral of the magnetic helicity density.
In all the cases mentioned above, either the magnetic helicity density was vanishing, so the spectral magnetic helicity was zero at all wavenumbers and the decay governed by the conservation of the Hosking integral, or the magnetic helicity density was finite and the spectral magnetic helicity had the same sign at all wavenumbers, so the decay was governed by the conservation of the mean magnetic helicity density. A special situation was studied in the work of Brandenburg, Kamada & Schober (Reference Brandenburg, Kamada and Schober2023b), where the magnetic helicity was finite, but it was balanced by fermion chirality of the opposite sign so that the net chirality was vanishing. For such a system, the decay was again successfully explained by the conservation of the Hosking integral, which was adapted to include the chirality from the fermions.
We have seen that the Hosking integral can be applied to broad ranges of systems where magnetic helicity is still important locally, but globally the net magnetic helicity vanishes. However, there is an important class of astrophysically relevant systems, where the magnetic field is not generated by magnetogenesis, as in the early universe, but by dynamo action. This means that some of the kinetic energy of turbulent motions is converted into magnetic energy. It is important to stress that, even if the velocity field were helical, i.e. if there is finite kinetic helicity in the system, as is generally the case when there is rotation and stratification of density and/or velocity, magnetic helicity conservation still precludes the generation of magnetic helicity, at least on dynamical time scales (Ji Reference Ji1999).
In the aforementioned helically driven large-scale dynamos, magnetic helicity can be generated at small scales, but it is then balanced by magnetic helicity at large scales so as to conserve magnetic helicity. Alternatively, we can also say that magnetic helicity is produced at large scales, for example by the tilting of buoyantly rising magnetic flux tubes in cyclonic convective events, as envisaged by Parker (Reference Parker1955). Magnetic helicity conservation then implies magnetic twist of opposite sign at smaller scales. In practice, because there is always finite magnetic diffusivity, which acts especially on small scales, the magnetic helicity from large scales will, after some time, dominate the total magnetic helicity owing to the loss at small scales where the magnetic helicity has the opposite sign. Therefore, there is always a small imbalance between the contributions from small and large length scales. It is therefore a situation that is only partially suited to the phenomenology involving the conservation of the Hosking integral.
If we now were to turn off the driving, the turbulence would gradually decay. This decay should then be governed by the conservation of both the Hosking integral and the mean magnetic helicity density. Both helical and non-helical cases lead to inverse cascading, where the magnetic field decays more slowly than the velocity field, leading ultimately to a magnetically dominated state. Such conditions could apply to the decay of a magnetic field produced in a proto-neutron star. There, we expect a turbulent dynamo to occur that is driven by convection (Thompson & Duncan Reference Thompson and Duncan1993). This would happen when the neutrino opacity is large enough to prevent neutrinos from escaping freely (Epstein Reference Epstein1979; Burrows & Lattimer Reference Burrows and Lattimer1986).
Another source of turbulence in proto-neutron stars could be the magnetorotational instability that results from the radially outward decreasing angular velocity gradient associated with collapsed material having an approximately constant angular momentum density (Guilet et al. Reference Guilet, Reboul-Salze, Raynaud, Bugli and Gallet2022). In both cases, the turbulence itself has kinetic helicity of opposite signs in the northern and southern hemispheres (negative in the north and positive in the south). In each hemisphere, this leads to dynamo action of the type described above, but the magnetic helicities have opposite signs not only in the two hemispheres, but also on small and large length scales. One would thus focus only on one hemisphere and ignore the interaction between north and south. The magnetic helicities from small and large length scales would then nearly cancel. Such fields have been called ‘bihelical’ and their decay properties were first studied by Yousef & Brandenburg (Reference Yousef and Brandenburg2003). They found that the positive and negative contributions rapidly mix and annihilate, and that the ratio of the magnetic helicity spectrum to the magnetic energy spectrum has local extrema at both small and large scales, although the latter is dominant in an absolute sense.
Since the net magnetic helicity of a bihelical magnetic field does not vanish exactly, and since the mean magnetic helicity itself is an important conserved quantity, we are confronted with a situation where the magnetic decay is governed by two conserved quantities. Investigating this aspect in a more controlled fashion is the main purpose of this paper.
In an earlier paper, Tevzadze et al. (Reference Tevzadze, Kisslinger, Brandenburg and Kahniashvili2012) studied a case with fractional helicity. They found that the correlation length developed a steeper growth (indicative of magnetic helicity domination) at a specific moment that depends on the value of the magnetic helicity as well as on the initial values of the magnetic energy and the magnetic correlation length. This consideration provided a quantitative estimate for the time of the switchover from non-helical to helical scalings. A similar estimate was provided by Hosking & Schekochihin (Reference Hosking and Schekochihin2021) based on the scaling of the Hosking integral $I_{H}$![]() . One may then ask whether the time of the switchover from a decay controlled by $I_{H}$
. One may then ask whether the time of the switchover from a decay controlled by $I_{H}$![]() to that controlled by the mean magnetic helicity density $I_{M}$
to that controlled by the mean magnetic helicity density $I_{M}$![]() can be computed based on dimensional arguments. Indeed, given that the quantity $I_{H}$
can be computed based on dimensional arguments. Indeed, given that the quantity $I_{H}$![]() has dimensions ${\rm cm}^9\ {\rm s}^{-4}$
has dimensions ${\rm cm}^9\ {\rm s}^{-4}$![]() and $I_{M}$
and $I_{M}$![]() has dimensions ${\rm cm}^3\ {\rm s}^{-2}$
has dimensions ${\rm cm}^3\ {\rm s}^{-2}$![]() (see Brandenburg (Reference Brandenburg2023), and note that the magnetic field is here understood to be in Alfvén units with dimensions ${\rm cm}\ {\rm s}^{-1}$
(see Brandenburg (Reference Brandenburg2023), and note that the magnetic field is here understood to be in Alfvén units with dimensions ${\rm cm}\ {\rm s}^{-1}$![]() ) a combination of $I_{H}$
) a combination of $I_{H}$![]() and $I_{M}$
and $I_{M}$![]() that yields a time would be $I_{H}^{1/2}I_{M}^{-3/2}$
that yields a time would be $I_{H}^{1/2}I_{M}^{-3/2}$![]() . It will turn out that this is indeed the time of switchover between the two regimes.
. It will turn out that this is indeed the time of switchover between the two regimes.
2 Our model
2.1 Basic equations
We simulate the compressible magnetohydrodynamic equations with an isothermal equation of state with constant sound speed $c_{s}$![]() , so the pressure $p$
, so the pressure $p$![]() and the density $\rho$
and the density $\rho$![]() are related by $p=\rho c _{s}^2$
are related by $p=\rho c _{s}^2$![]() . The equations for the magnetic vector potential $\boldsymbol {A}$
. The equations for the magnetic vector potential $\boldsymbol {A}$![]() , the velocity $\boldsymbol {U}$
, the velocity $\boldsymbol {U}$![]() and the logarithmic density $\ln \rho$
and the logarithmic density $\ln \rho$![]() are
are
where ${\rm D} {}/{\rm D} {} t=\partial /\partial t+\boldsymbol {U}\boldsymbol {\cdot }{\boldsymbol {\nabla }}$![]() is the advective derivative, $\boldsymbol {B}={\boldsymbol {\nabla }}\times \boldsymbol {A}$
is the advective derivative, $\boldsymbol {B}={\boldsymbol {\nabla }}\times \boldsymbol {A}$![]() is the magnetic field, $\boldsymbol {J}={\boldsymbol {\nabla }}\times \boldsymbol {B}/\mu _0$
is the magnetic field, $\boldsymbol {J}={\boldsymbol {\nabla }}\times \boldsymbol {B}/\mu _0$![]() is the current density, $\mu _0$
is the current density, $\mu _0$![]() is the vacuum permeability, $\nu$
is the vacuum permeability, $\nu$![]() is the viscosity and ${\boldsymbol {\textit {S}}}_{ij}=(\partial _i U_j+\partial _j U_i)/2-\delta _{ij}{\boldsymbol {\nabla }}\boldsymbol {\cdot }\boldsymbol {U}/3$
is the viscosity and ${\boldsymbol {\textit {S}}}_{ij}=(\partial _i U_j+\partial _j U_i)/2-\delta _{ij}{\boldsymbol {\nabla }}\boldsymbol {\cdot }\boldsymbol {U}/3$![]() are the components of the traceless rate-of-strain tensor $\boldsymbol{\mathsf{S}}$
are the components of the traceless rate-of-strain tensor $\boldsymbol{\mathsf{S}}$![]() . Our computational domain is a periodic cube of size $L^3$
. Our computational domain is a periodic cube of size $L^3$![]() , and $k_1=2{\rm \pi} /L$
, and $k_1=2{\rm \pi} /L$![]() is the smallest wavenumber. Since the mass in the domain does not change, the volume-averaged density is constant in time, i.e. $\langle \rho \rangle ={\rm const.} {}\equiv \rho _0$
is the smallest wavenumber. Since the mass in the domain does not change, the volume-averaged density is constant in time, i.e. $\langle \rho \rangle ={\rm const.} {}\equiv \rho _0$![]() . Here and below, angle brackets denote volume averaging.
. Here and below, angle brackets denote volume averaging.
2.2 Initial conditions
In our idealized studies, we focus on the decay governed by two conserved quantities (Hosking integral and mean magnetic helicity density). We construct an initial magnetic vector potential in Fourier space as $\tilde {\boldsymbol {A}}(k)={\boldsymbol{\mathsf{R}}}(k;\varsigma )\tilde {\boldsymbol {A}}^{\mathrm {nhel}}$![]() , where
, where
is a matrix with $\hat {k}_i$![]() being the components of the unit vector $\hat {\boldsymbol {k}}=\boldsymbol {k}/k$
being the components of the unit vector $\hat {\boldsymbol {k}}=\boldsymbol {k}/k$![]() , $|\varsigma |\leqslant 1$
, $|\varsigma |\leqslant 1$![]() is a non-dimensional parameter that quantifies the fractional helicity and $\tilde {\boldsymbol {A}}^\mathrm {nhel}$
is a non-dimensional parameter that quantifies the fractional helicity and $\tilde {\boldsymbol {A}}^\mathrm {nhel}$![]() is a non-helical field with random phases and possesses the desired spectrum for the magnetic field ${\rm Sp}(\boldsymbol {B})=k^2{\rm Sp}(\boldsymbol {A})$
is a non-helical field with random phases and possesses the desired spectrum for the magnetic field ${\rm Sp}(\boldsymbol {B})=k^2{\rm Sp}(\boldsymbol {A})$![]() , i.e.
, i.e.
where $A_0$![]() is an amplitude, $k_0$
is an amplitude, $k_0$![]() denotes the initial position of the spectral peak, $\alpha$
denotes the initial position of the spectral peak, $\alpha$![]() is the subinertial range slope (here always $\alpha =4$
is the subinertial range slope (here always $\alpha =4$![]() ) and the inertial range has a $k^{-5/3}$
) and the inertial range has a $k^{-5/3}$![]() spectrum. Note that $\boldsymbol {A}$
spectrum. Note that $\boldsymbol {A}$![]() is by construction periodic. Therefore, $\boldsymbol {B}={\boldsymbol {\nabla }}\times \boldsymbol {A}$
is by construction periodic. Therefore, $\boldsymbol {B}={\boldsymbol {\nabla }}\times \boldsymbol {A}$![]() has zero mean field. At the end of this paper, we also briefly discuss a case with a finite mean magnetic field.
has zero mean field. At the end of this paper, we also briefly discuss a case with a finite mean magnetic field.
The strength of the magnetic field can be characterized by the Alfvén speed, $v_{A}=B_{\rm rms}/\sqrt {\mu _0\rho _0}$![]() , which is here based on the mean density. For $\varsigma \neq 0$
, which is here based on the mean density. For $\varsigma \neq 0$![]() , we have a finite magnetic helicity and expect then the decay to be governed by both the Hosking integral and the mean magnetic helicity density.
, we have a finite magnetic helicity and expect then the decay to be governed by both the Hosking integral and the mean magnetic helicity density.
In (2.5), ${\rm Sp}(\cdot )$![]() denotes a shell integrated spectrum. This operation will also be applied to the local, gauge-dependent magnetic helicity density $h=\boldsymbol {A}\boldsymbol {\cdot }\boldsymbol {B}$
denotes a shell integrated spectrum. This operation will also be applied to the local, gauge-dependent magnetic helicity density $h=\boldsymbol {A}\boldsymbol {\cdot }\boldsymbol {B}$![]() , so that ${\rm Sp}(h)=(k^2/8{\rm \pi} ^3L^3)\oint _{4{\rm \pi} }|\tilde {h}|^2\,{\rm d} {}\varOmega _k$
, so that ${\rm Sp}(h)=(k^2/8{\rm \pi} ^3L^3)\oint _{4{\rm \pi} }|\tilde {h}|^2\,{\rm d} {}\varOmega _k$![]() . The tilde marks a quantity in Fourier space, and $\varOmega _k$
. The tilde marks a quantity in Fourier space, and $\varOmega _k$![]() is the solid angle in Fourier space, so that $\int {\rm Sp}(h)\,{\rm d} {} k=\langle h^2\rangle$
is the solid angle in Fourier space, so that $\int {\rm Sp}(h)\,{\rm d} {} k=\langle h^2\rangle$![]() , and likewise for $\int {\rm Sp}(\boldsymbol {B})\,{\rm d} {} k=\langle \boldsymbol {B}^2\rangle$
, and likewise for $\int {\rm Sp}(\boldsymbol {B})\,{\rm d} {} k=\langle \boldsymbol {B}^2\rangle$![]() . Owing to the integration over shells in three-dimensional wavenumber space, the spectrum of a spatially random ($\delta$
. Owing to the integration over shells in three-dimensional wavenumber space, the spectrum of a spatially random ($\delta$![]() correlated) field is proportional to $k^2$
correlated) field is proportional to $k^2$![]() . This is indeed the case for a globally non-helical field, where $\langle h\rangle =0$
. This is indeed the case for a globally non-helical field, where $\langle h\rangle =0$![]() .
.
2.3 Definitions of the Hosking integral
The Hosking integral $I_{H}$![]() is defined as the asymptotic limit of the magnetic helicity density correlation integral:
is defined as the asymptotic limit of the magnetic helicity density correlation integral:
for scales $R$![]() large compared with the correlation length $\xi _{M}$
large compared with the correlation length $\xi _{M}$![]() of the turbulence, but small compared with the system size $L$
of the turbulence, but small compared with the system size $L$![]() . Here, $V_R=4{\rm \pi} R^3/3$
. Here, $V_R=4{\rm \pi} R^3/3$![]() is the volume of a sphere of radius $R$
is the volume of a sphere of radius $R$![]() . For small values of $R$
. For small values of $R$![]() , the function ${\mathcal {I}}_{H}(R)$
, the function ${\mathcal {I}}_{H}(R)$![]() increases proportional to $R^3$
increases proportional to $R^3$![]() , but for large $R$
, but for large $R$![]() , it levels off when there is no net magnetic helicity. However, as explained in Hosking & Schekochihin (Reference Hosking and Schekochihin2021), this is different for finite magnetic helicity, as is discussed below. In practice, the value of $R$
, it levels off when there is no net magnetic helicity. However, as explained in Hosking & Schekochihin (Reference Hosking and Schekochihin2021), this is different for finite magnetic helicity, as is discussed below. In practice, the value of $R$![]() is chosen empirically and must always be small compared with the size of the domain.
is chosen empirically and must always be small compared with the size of the domain.
Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) devised and compared different methods for computing $\mathcal {I}_{H}(R)$![]() . These methods are all based on the Fourier transform of $h$
. These methods are all based on the Fourier transform of $h$![]() . Particularly simple is what they called the box-counting method for a spherical volume with radius $R$
. Particularly simple is what they called the box-counting method for a spherical volume with radius $R$![]() . This allowed them to rewrite (2.6) as a weighted integral over ${\rm Sp}(h)$
. This allowed them to rewrite (2.6) as a weighted integral over ${\rm Sp}(h)$![]() :
:
where
and $j_1(x)=(\sin x-x\cos x)/x^2$![]() is a spherical Bessel function.
is a spherical Bessel function.
2.4 Input and diagnostic parameters of the model
Important input parameters of the model are the ratio of the initial Alfvén speed to the sound speed, $v_{A0}/c_{s}$![]() . In the presence of an imposed mean field, $\boldsymbol {B}_{m}=B_{m}\hat {\boldsymbol {x}} {}$
. In the presence of an imposed mean field, $\boldsymbol {B}_{m}=B_{m}\hat {\boldsymbol {x}} {}$![]() , a case discussed at the end of the paper, the corresponding Alfvén speed is denoted by $v_{\rm Am}$
, a case discussed at the end of the paper, the corresponding Alfvén speed is denoted by $v_{\rm Am}$![]() . To obtain information about the turbulent decay that is independent of the size and shape of the computational domain, we must choose the value of $k_0/k_1$
. To obtain information about the turbulent decay that is independent of the size and shape of the computational domain, we must choose the value of $k_0/k_1$![]() to be sufficiently large. However, it should also not be chosen too large, because it would diminish the range of wavenumbers between $k_0$
to be sufficiently large. However, it should also not be chosen too large, because it would diminish the range of wavenumbers between $k_0$![]() and the largest wavenumber in the domain, which is called the Nyquist wavenumber, $k_\mathrm {Ny}=k_1 N/2$
and the largest wavenumber in the domain, which is called the Nyquist wavenumber, $k_\mathrm {Ny}=k_1 N/2$![]() , where $N$
, where $N$![]() is the number of mesh points. The sensitivity of the results on the choice of $k_0$
is the number of mesh points. The sensitivity of the results on the choice of $k_0$![]() has been studied on various occasions (e.g. Zhou et al. Reference Zhou, Sharma and Brandenburg2022). A reasonable compromise that still allows for sufficiently large Reynolds numbers seems to be $k_0/k_1=60$
has been studied on various occasions (e.g. Zhou et al. Reference Zhou, Sharma and Brandenburg2022). A reasonable compromise that still allows for sufficiently large Reynolds numbers seems to be $k_0/k_1=60$![]() . This is the value that is used for the main run in the present paper, but we also present some results with $k_0/k_1=30$
. This is the value that is used for the main run in the present paper, but we also present some results with $k_0/k_1=30$![]() ; see table 1 for a summary of runs presented in this paper.
; see table 1 for a summary of runs presented in this paper.
Table 1. Summary of runs presented in this paper. The arrows indicate the change from the beginning to the end of the run.

To characterize the degree of compressibility and the vigour of turbulence, we quote the Mach and Lundquist numbers:
Since our model is spatially homogeneous, it can be characterized by the magnetic energy and helicity spectra, $E_{M}(k,t)$![]() and $H_{M}(k,t)$
and $H_{M}(k,t)$![]() , respectively. They are normalized such that their integrals give the mean magnetic energy and helicity densities, ${\mathcal {E}}_{M}\equiv \int E _{M}(k,t)\,{\rm d} {} k=\langle \boldsymbol {B}^2\rangle /2\mu _0$
, respectively. They are normalized such that their integrals give the mean magnetic energy and helicity densities, ${\mathcal {E}}_{M}\equiv \int E _{M}(k,t)\,{\rm d} {} k=\langle \boldsymbol {B}^2\rangle /2\mu _0$![]() and $I_{M}\equiv \int H _{M}(k,t)\,{\rm d} {} k=\langle \boldsymbol {A}\boldsymbol {\cdot }\boldsymbol {B}\rangle$
and $I_{M}\equiv \int H _{M}(k,t)\,{\rm d} {} k=\langle \boldsymbol {A}\boldsymbol {\cdot }\boldsymbol {B}\rangle$![]() , respectively.Footnote 1
, respectively.Footnote 1
The position of the peak of the spectrum is characterized by the inverse magnetic integral scale, $k_\mathrm {peak}=\xi _{M}^{-1}$![]() , where $\xi _{M}$
, where $\xi _{M}$![]() is here defined as
is here defined as
Of particular importance are the time dependencies $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() , which, in turn, are characterized by the instantaneous scaling exponents $q(t)={\rm d} {}\ln \xi _{M}/{\rm d} {}\ln t$
, which, in turn, are characterized by the instantaneous scaling exponents $q(t)={\rm d} {}\ln \xi _{M}/{\rm d} {}\ln t$![]() and $p(t)=-{\rm d} {}\ln {\mathcal {E}}_{M}/{\rm d} {}\ln t$
and $p(t)=-{\rm d} {}\ln {\mathcal {E}}_{M}/{\rm d} {}\ln t$![]() . The relative magnetic helicity can be computed as the non-dimensional ratio $I_{M}/2\xi _{M}{\mathcal {E}}_{M}$
. The relative magnetic helicity can be computed as the non-dimensional ratio $I_{M}/2\xi _{M}{\mathcal {E}}_{M}$![]() , which is between $-1$
, which is between $-1$![]() and $+1$
and $+1$![]() .
.
The relevant information that quantifies the Hosking integral is the first non-vanishing coefficient in the Taylor expansion:
see Hosking & Schekochihin (Reference Hosking and Schekochihin2021), Schekochihin (Reference Schekochihin2022) and Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for details. This is also the primary method used here to determine the value of $I_{H}$![]() ; see Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for a comparison between different methods. We confirm that $2{\rm \pi} ^2 {\rm Sp}(h)/k^2$
; see Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for a comparison between different methods. We confirm that $2{\rm \pi} ^2 {\rm Sp}(h)/k^2$![]() has an approximately flat part for small values of $k$
has an approximately flat part for small values of $k$![]() and use its value at $k=k_1$
and use its value at $k=k_1$![]() to measure $I_{H}$
to measure $I_{H}$![]() . Below, we also confirm that $I_{H}$
. Below, we also confirm that $I_{H}$![]() is nearly independent of time; see Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for quantitative assessment of its invariance in the ideal limit. Note that, since $\int {\rm Sp}(h)\,{\rm d} {} k=\langle h^2\rangle$
is nearly independent of time; see Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for quantitative assessment of its invariance in the ideal limit. Note that, since $\int {\rm Sp}(h)\,{\rm d} {} k=\langle h^2\rangle$![]() , which has dimensions $({\rm cm}^3\ {\rm s}^{-2})^2$
, which has dimensions $({\rm cm}^3\ {\rm s}^{-2})^2$![]() , ${\rm Sp}(h)$
, ${\rm Sp}(h)$![]() has dimensions ${\rm cm}^7\ {\rm s}^{-4}$
has dimensions ${\rm cm}^7\ {\rm s}^{-4}$![]() and therefore $I_{H}$
and therefore $I_{H}$![]() has dimensions ${\rm cm}^9\ {\rm s}^{-4}$
has dimensions ${\rm cm}^9\ {\rm s}^{-4}$![]() , as expected.
, as expected.
To facilitate comparison with other work, it is useful to present our results in non-dimensional form. The time used in the numerical simulations is made non- dimensional by plotting the evolution versus $c_{s} k_1 t$![]() , which is convenient for numerical reasons, because $c_{s}$
, which is convenient for numerical reasons, because $c_{s}$![]() and $k_1$
and $k_1$![]() are constant in time. However, physically more meaningful would be a non-dimensionalization by using the Alfvén speed and the inverse correlation length. Both are time dependent, but the values $v_\mathrm {Ae}$
are constant in time. However, physically more meaningful would be a non-dimensionalization by using the Alfvén speed and the inverse correlation length. Both are time dependent, but the values $v_\mathrm {Ae}$![]() and $k_{e}$
and $k_{e}$![]() at the end of the simulations seem to be most meaningful.
at the end of the simulations seem to be most meaningful.
2.5 Run time and scale separation
To obtain meaningful results, two important constraints need to be obeyed. First, the value of ${\textit {Lu}}$![]() needs to be large enough so that we are in the regime of developed turbulence. Second, the subinertial range must always be large enough so that, by the end of the run, its slope is not affected by finite size effects of the computational domain. This automatically limits the maximum run time below which our results can still be meaningful. Both constraints can only be obeyed in the limit of infinite resolution. In practice, the largest resolution that is presently feasible is typically $2048^3$
needs to be large enough so that we are in the regime of developed turbulence. Second, the subinertial range must always be large enough so that, by the end of the run, its slope is not affected by finite size effects of the computational domain. This automatically limits the maximum run time below which our results can still be meaningful. Both constraints can only be obeyed in the limit of infinite resolution. In practice, the largest resolution that is presently feasible is typically $2048^3$![]() mesh points (Zhou et al. Reference Zhou, Sharma and Brandenburg2022), but this large resolution does already constrain the number of experiments that can reasonably be performed. Therefore, we use for most of our simulations a lower resolution of $N^3=1024^3$
mesh points (Zhou et al. Reference Zhou, Sharma and Brandenburg2022), but this large resolution does already constrain the number of experiments that can reasonably be performed. Therefore, we use for most of our simulations a lower resolution of $N^3=1024^3$![]() mesh points. In that case, the largest wavenumber in the domain is $k_\mathrm {Ny}=k_1 N/2=512\,k_1$
mesh points. In that case, the largest wavenumber in the domain is $k_\mathrm {Ny}=k_1 N/2=512\,k_1$![]() . As discussed above, this led us to the compromise of choosing the values 30 and 60 for the scale separation ratio $k_0/k_1$
. As discussed above, this led us to the compromise of choosing the values 30 and 60 for the scale separation ratio $k_0/k_1$![]() , so $k_0/k_\mathrm {Ny}=17$
, so $k_0/k_\mathrm {Ny}=17$![]() –$8.5$
–$8.5$![]() , leaving barely enough dynamical range for turbulence to develop.
, leaving barely enough dynamical range for turbulence to develop.
3 Results
In the present context, we have to deal with two conserved quantities, namely the Hosking integral $I_{H}$![]() and the mean magnetic helicity density $I_{M}=\langle \boldsymbol {A}\boldsymbol {\cdot }\boldsymbol {B}\rangle$
and the mean magnetic helicity density $I_{M}=\langle \boldsymbol {A}\boldsymbol {\cdot }\boldsymbol {B}\rangle$![]() . The former case has been studied extensively in recent years. Specifically, Brandenburg & Larsson (Reference Brandenburg and Larsson2023) and Brandenburg et al. (Reference Brandenburg, Sharma and Vachaspati2023c) found
. The former case has been studied extensively in recent years. Specifically, Brandenburg & Larsson (Reference Brandenburg and Larsson2023) and Brandenburg et al. (Reference Brandenburg, Sharma and Vachaspati2023c) found
The hope is that the coefficients in these expressions are universal, but it should be noted that they have not yet been verified in other contexts.
3.1 Decay controlled by mean and fluctuating magnetic helicities
In the helical case with $I_{M}\neq 0$![]() , we have $\xi _{M}\propto t^{2/3}$
, we have $\xi _{M}\propto t^{2/3}$![]() and ${\mathcal {E}}_{M}\propto t^{-2/3}$
and ${\mathcal {E}}_{M}\propto t^{-2/3}$![]() (Hatori Reference Hatori1984; Biskamp & Müller Reference Biskamp and Müller1999; Brandenburg & Kahniashvili Reference Brandenburg and Kahniashvili2017). In the present context, the pre-factors are important. Using the data from figures 1(c) and 2(c) of Brandenburg & Kahniashvili (Reference Brandenburg and Kahniashvili2017), here referred to as Run A, we find
(Hatori Reference Hatori1984; Biskamp & Müller Reference Biskamp and Müller1999; Brandenburg & Kahniashvili Reference Brandenburg and Kahniashvili2017). In the present context, the pre-factors are important. Using the data from figures 1(c) and 2(c) of Brandenburg & Kahniashvili (Reference Brandenburg and Kahniashvili2017), here referred to as Run A, we find
Generally, we can write
where the index $i$![]() in the integrals $I_i$
in the integrals $I_i$![]() and the coefficients $C_{i}^{(\xi )}$
and the coefficients $C_{i}^{(\xi )}$![]() , $C_{i}^{({\mathcal {E}})}$
, $C_{i}^{({\mathcal {E}})}$![]() and $C_{i}^{({E})}$
and $C_{i}^{({E})}$![]() stands for $M$
stands for $M$![]() or $H$
or $H$![]() for magnetic helicity and Hosking scalings, respectively, and $\sigma$
for magnetic helicity and Hosking scalings, respectively, and $\sigma$![]() is the exponent with which length enters in $I_{i}$
is the exponent with which length enters in $I_{i}$![]() : $\sigma =1/3$
: $\sigma =1/3$![]() for the magnetic helicity density ($i={M}$
for the magnetic helicity density ($i={M}$![]() ) and $\sigma =1/9$
) and $\sigma =1/9$![]() for the Hosking integral ($i={H}$
for the Hosking integral ($i={H}$![]() ); see table 2 for a summary of the coefficients.Footnote 2
); see table 2 for a summary of the coefficients.Footnote 2
Table 2. Summary of the coefficients characterizing the decays governed by the conservation of magnetic helicity ($i={M}$![]() ) and the Hosking integral ($i={H}$
) and the Hosking integral ($i={H}$![]() ).
).

In figure 1, we show the magnetic energy spectra, as well as compensated evolutions of $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() for the maximally helical run (Run A). We see that the peak of ${\mathcal {E}}_{M}(t)$
for the maximally helical run (Run A). We see that the peak of ${\mathcal {E}}_{M}(t)$![]() remains underneath a nearly flat envelope (its slope is $\beta =0$
remains underneath a nearly flat envelope (its slope is $\beta =0$![]() ), as is expected for a fully helical turbulent decay at late times. The compensated evolutions of $\xi _{M}(t)$
), as is expected for a fully helical turbulent decay at late times. The compensated evolutions of $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() are not yet fully converged towards the end of that run (the lines are not yet flat). This is partially caused by the insufficient scale separation between the box wavenumber $k_1$
are not yet fully converged towards the end of that run (the lines are not yet flat). This is partially caused by the insufficient scale separation between the box wavenumber $k_1$![]() and that of the spectral peak by the end of the run. Nevertheless, we can read off the approximate values $C_{M}^{(\xi )}\approx 0.12$
and that of the spectral peak by the end of the run. Nevertheless, we can read off the approximate values $C_{M}^{(\xi )}\approx 0.12$![]() and $C_{M}^{({\mathcal {E}})}\approx 4.3$
and $C_{M}^{({\mathcal {E}})}\approx 4.3$![]() towards the end of the run. The values of these coefficients are revisited later in this paper.
towards the end of the run. The values of these coefficients are revisited later in this paper.

Figure 1. (a) Magnetic energy spectra, as well as compensated evolutions of (b) $\xi _{M}(t)$![]() and (c) ${\mathcal {E}}_{M}(t)$
and (c) ${\mathcal {E}}_{M}(t)$![]() for the maximally helical run of figure 2(c) of Brandenburg & Kahniashvili (Reference Brandenburg and Kahniashvili2017), here referred to as Run A. In (a), the red symbols denote the spectral peaks.
for the maximally helical run of figure 2(c) of Brandenburg & Kahniashvili (Reference Brandenburg and Kahniashvili2017), here referred to as Run A. In (a), the red symbols denote the spectral peaks.
In figure 2, we again show the compensated evolutions of $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() , but now for Run B, which is nearly perfectly non-helical ($\varsigma =0.003$
, but now for Run B, which is nearly perfectly non-helical ($\varsigma =0.003$![]() ) and has $k_0/k_1=30$
) and has $k_0/k_1=30$![]() . The resulting coefficients are close to those estimated previously, namely $C_{H}^{(\xi )}\approx 0.12$
. The resulting coefficients are close to those estimated previously, namely $C_{H}^{(\xi )}\approx 0.12$![]() and $C_{H}^{({\mathcal {E}})}\approx 4.7$
and $C_{H}^{({\mathcal {E}})}\approx 4.7$![]() . This supports the previous hypotheses of Brandenburg & Larsson (Reference Brandenburg and Larsson2023) and Brandenburg et al. (Reference Brandenburg, Sharma and Vachaspati2023c) that these coefficients may indeed be universal.
. This supports the previous hypotheses of Brandenburg & Larsson (Reference Brandenburg and Larsson2023) and Brandenburg et al. (Reference Brandenburg, Sharma and Vachaspati2023c) that these coefficients may indeed be universal.

Figure 2. Evolution of $\xi _{M}(t)$![]() (a,b) and ${\mathcal {E}}_{M}(t)$
(a,b) and ${\mathcal {E}}_{M}(t)$![]() (c,d) for Run B with $k_0/k_1=30$
(c,d) for Run B with $k_0/k_1=30$![]() and $\varsigma =0.003$
and $\varsigma =0.003$![]() , compensated by the expected evolution if the decay is controlled either by $I_{H}$
, compensated by the expected evolution if the decay is controlled either by $I_{H}$![]() (a,c) or by $I_{M}$
(a,c) or by $I_{M}$![]() (b,d). The dashed line denotes the use of $I_{M}$
(b,d). The dashed line denotes the use of $I_{M}$![]() at the end of the run, while for the solid line, the time-dependent value was taken.
at the end of the run, while for the solid line, the time-dependent value was taken.
To determine the value of $I_{H}(t)$![]() , we plot in figure 3 the evolutions of $(2{\rm \pi} ^2/k^2)\, {\rm Sp}(h)$
, we plot in figure 3 the evolutions of $(2{\rm \pi} ^2/k^2)\, {\rm Sp}(h)$![]() (normalized by $v_\mathrm {Ae}^4/k_{e}^5$
(normalized by $v_\mathrm {Ae}^4/k_{e}^5$![]() ) for $k/k_1=1$
) for $k/k_1=1$![]() , 2 and 3 for Run B. We see that for $k/k_1=1$
, 2 and 3 for Run B. We see that for $k/k_1=1$![]() , the result shows a nearly negligible decline proportional to $t^{-0.07}$
, the result shows a nearly negligible decline proportional to $t^{-0.07}$![]() . Note that, in units of $v_\mathrm {Ae}^4/k_{e}^5$
. Note that, in units of $v_\mathrm {Ae}^4/k_{e}^5$![]() , the value of $I_{H}$
, the value of $I_{H}$![]() is about 500.
is about 500.

Figure 3. Evolutions of $(2{\rm \pi} ^2/k^2)\, {\rm Sp}(h)$![]() , normalized by $v_\mathrm {Ae}^4/k_{e}^5$
, normalized by $v_\mathrm {Ae}^4/k_{e}^5$![]() , for $k/k_1=1$
, for $k/k_1=1$![]() (solid line), 2 (dashed-dotted line) and 3 (dashed line), for the nearly non-helical Run B with $\varsigma =0.003$
(solid line), 2 (dashed-dotted line) and 3 (dashed line), for the nearly non-helical Run B with $\varsigma =0.003$![]() and $k_0/k_1=30$
and $k_0/k_1=30$![]() .
.
3.2 Decay controlled by $I_{M}$ and $I_{H}$
and $I_{H}$
If both $I_{M}$![]() and $I_{H}$
and $I_{H}$![]() control the decay, we have a combination of the two decay laws such that the late times are always controlled by the more strongly conserved quantity, i.e. by $I_{M}$
control the decay, we have a combination of the two decay laws such that the late times are always controlled by the more strongly conserved quantity, i.e. by $I_{M}$![]() . One might expect that the resulting expression for the combination of the decay laws (3.1a–c) and (3.1a–c) is given by the sum of both expressions. This would be analogous to the way how in radiation transport the cooling time is given by the sum of the cooling times for the optically thick and thin cases; see (7) of Brandenburg & Das (Reference Brandenburg and Das2020). In the present case, this would translate to
. One might expect that the resulting expression for the combination of the decay laws (3.1a–c) and (3.1a–c) is given by the sum of both expressions. This would be analogous to the way how in radiation transport the cooling time is given by the sum of the cooling times for the optically thick and thin cases; see (7) of Brandenburg & Das (Reference Brandenburg and Das2020). In the present case, this would translate to
Since the second terms involving $I_{H}$![]() are initially larger, but their contributions to $\xi _{M}$
are initially larger, but their contributions to $\xi _{M}$![]() grow more slowly and that to ${\mathcal {E}}_{M}$
grow more slowly and that to ${\mathcal {E}}_{M}$![]() decay faster than the first terms, one expects their contributions to become subdominant after some time. Thus, the magnetic helicity will always survive and be the dominant contribution to explaining the decay.
decay faster than the first terms, one expects their contributions to become subdominant after some time. Thus, the magnetic helicity will always survive and be the dominant contribution to explaining the decay.
To examine now a run where the decay is controlled by both $I_{M}$![]() and $I_{H}$
and $I_{H}$![]() , we now increase the initial fractional helicity slightly from 0.003 to 0.01; see figure 4 for magnetic energy spectra at different times for Run C. Note that the peaks of the spectra evolve at first underneath an envelope with the slope $\beta =3/2$
, we now increase the initial fractional helicity slightly from 0.003 to 0.01; see figure 4 for magnetic energy spectra at different times for Run C. Note that the peaks of the spectra evolve at first underneath an envelope with the slope $\beta =3/2$![]() , as expected for a decay controlled by $I_{H}$
, as expected for a decay controlled by $I_{H}$![]() . At later times, however, the envelope becomes flat (slope $\beta =0$
. At later times, however, the envelope becomes flat (slope $\beta =0$![]() ), as expected for a decay controlled by $I_{M}$
), as expected for a decay controlled by $I_{M}$![]() .
.

Figure 4. Magnetic energy spectra for Run C with $k_0/k_1=60$![]() and $\varsigma =0.01$
and $\varsigma =0.01$![]() at times $v_\mathrm {Ae} k_{e}\,t=0.07$
at times $v_\mathrm {Ae} k_{e}\,t=0.07$![]() , 0.18, 0.40, 0.82, 1.65, 3.3, 6.1, 11.1 and 20.7.
, 0.18, 0.40, 0.82, 1.65, 3.3, 6.1, 11.1 and 20.7.
In figure 5, we show the evolutions of $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() for Run C, compensated by $t^{-2/3}$
for Run C, compensated by $t^{-2/3}$![]() and $t^{2/3}$
and $t^{2/3}$![]() , respectively, as well as $t^{-4/9}$
, respectively, as well as $t^{-4/9}$![]() and $t^{10/9}$
and $t^{10/9}$![]() , respectively. We see that now the curves compensated by $t^{-2/3}$
, respectively. We see that now the curves compensated by $t^{-2/3}$![]() and $t^{2/3}$
and $t^{2/3}$![]() , respectively, become nearly constant, as expected for a decay that is governed by magnetic helicity conservation. Specifically, we find $\xi _{M}/(I_{M}^{1/3}\,t^{2/3})\approx 0.14$
, respectively, become nearly constant, as expected for a decay that is governed by magnetic helicity conservation. Specifically, we find $\xi _{M}/(I_{M}^{1/3}\,t^{2/3})\approx 0.14$![]() and ${\mathcal {E}}_{M}/(I_{M}^{2/3}\,t^{-2/3})\approx 4.0$
and ${\mathcal {E}}_{M}/(I_{M}^{2/3}\,t^{-2/3})\approx 4.0$![]() . During a short intermediate interval, however, we see that the curves compensated by $t^{-4/9}$
. During a short intermediate interval, however, we see that the curves compensated by $t^{-4/9}$![]() and $t^{10/9}$
and $t^{10/9}$![]() , respectively, show brief plateaus around $v_\mathrm {Ae}k_{e}t=1$
, respectively, show brief plateaus around $v_\mathrm {Ae}k_{e}t=1$![]() with $\xi _{M}/(I_{H}^{1/9}\,t^{4/9})\approx 0.12$
with $\xi _{M}/(I_{H}^{1/9}\,t^{4/9})\approx 0.12$![]() and ${\mathcal {E}}_{M}/(I_{H}^{2/9}\,t^{-10/9})\approx 4.0$
and ${\mathcal {E}}_{M}/(I_{H}^{2/9}\,t^{-10/9})\approx 4.0$![]() .
.

Figure 5. Similar to figure 2, but for Run C with $k_0/k_1=60$![]() and $\varsigma =0.01$
and $\varsigma =0.01$![]() .
.
3.3 Improved fits with $I_{M}$ and $I_{H}$
and $I_{H}$
We have seen that the limiting cases where the decay is controlled either by $I_{M}$![]() or by $I_{H}$
or by $I_{H}$![]() are well reproduced by (3.1a–c). It turns out, however, that the combined fits given by (3.4) and (3.5) are not very accurate. Improved fits can be obtained by using large weighting exponents for both contributions, i.e.
are well reproduced by (3.1a–c). It turns out, however, that the combined fits given by (3.4) and (3.5) are not very accurate. Improved fits can be obtained by using large weighting exponents for both contributions, i.e.
The result is shown in figure 6 for Run C, where we show that $s=10$![]() yields satisfactory fits, while $s=2$
yields satisfactory fits, while $s=2$![]() and $s=1$
and $s=1$![]() (our original hypothesis) are poor. The fact that the coefficients for both parts are different from those of the individual fits and that they happen to be $4.0$
(our original hypothesis) are poor. The fact that the coefficients for both parts are different from those of the individual fits and that they happen to be $4.0$![]() in (3.7), but different from each other in (3.6), is probably just by chance and reflect that degree of uncertainty of these values.
in (3.7), but different from each other in (3.6), is probably just by chance and reflect that degree of uncertainty of these values.
It is important to emphasize that the limit $s\to \infty$![]() corresponds to
corresponds to
These expressions yield discontinuities in the derivative. An advantage of such expressions is that one can clearly see the regimes of validity of both expressions. The critical times when characterizing the crossover from Hosking scaling to magnetic helicity scaling are given by
It would be plausible to assume that both times should equal each other. The fact that they are not equal to each other might hint, again, at the possibility that the precise values of these coefficients are still uncertain. On the other hand, looking at figure 5, it is actually true that $\xi _{M}$![]() approaches the $I_{M}$
approaches the $I_{M}$![]() -dominated scaling by a factor two earlier than ${\mathcal {E}}_{M}$
-dominated scaling by a factor two earlier than ${\mathcal {E}}_{M}$![]() . A possible explanation for this behaviour could lie in the fact that the spectral shapes change as the system becomes fully helical. We return to this in § 3.4, where we discuss the spectral shapes in more detail.
. A possible explanation for this behaviour could lie in the fact that the spectral shapes change as the system becomes fully helical. We return to this in § 3.4, where we discuss the spectral shapes in more detail.
We recall that an essential assumption in our dimensional argument was the fact that the magnetic field is understood to be in Alfvén units and thus has dimensions of ${\rm cm}\ {\rm s}^{-1}$![]() . In neutron star crusts, by contrast, where the magnetic field is governed by the Hall effect (Goldreich & Reisenegger Reference Goldreich and Reisenegger1992), it has units of ${\rm cm}^2\ {\rm s}^{-1}$
. In neutron star crusts, by contrast, where the magnetic field is governed by the Hall effect (Goldreich & Reisenegger Reference Goldreich and Reisenegger1992), it has units of ${\rm cm}^2\ {\rm s}^{-1}$![]() , so $[I_{M}]={\rm cm}^5\ {\rm s}^{-2}$
, so $[I_{M}]={\rm cm}^5\ {\rm s}^{-2}$![]() and $[I_{H}]={\rm cm}^{13}\ {\rm s}^{-4}$
and $[I_{H}]={\rm cm}^{13}\ {\rm s}^{-4}$![]() (Brandenburg Reference Brandenburg2023), so $t_\xi$
(Brandenburg Reference Brandenburg2023), so $t_\xi$![]() and $t_{\mathcal {E}}$
and $t_{\mathcal {E}}$![]() are now proportional to $I_{H}^{5/6}I_{M}^{-13/6}$
are now proportional to $I_{H}^{5/6}I_{M}^{-13/6}$![]() , so both exponents are larger than in the ordinary magnetohydrodynamic case; cf. (3.10) and (3.11). An example of the corresponding switch between the two regimes was presented in figure 10(b) of Brandenburg (Reference Brandenburg2020).
, so both exponents are larger than in the ordinary magnetohydrodynamic case; cf. (3.10) and (3.11). An example of the corresponding switch between the two regimes was presented in figure 10(b) of Brandenburg (Reference Brandenburg2020).
3.4 Collapsed spectra
The quality of the fits of (3.6) and (3.7) for $s=1$![]() and $s\to \infty$
and $s\to \infty$![]() can be examined further by computing compensated spectra. This is shown in figure 7, where the abscissa is scaled with $\xi _{M}(t)$
can be examined further by computing compensated spectra. This is shown in figure 7, where the abscissa is scaled with $\xi _{M}(t)$![]() and the ordinate with $[{\mathcal {E}}_{M}(t)\xi _{M}(t)]^{-1}$
and the ordinate with $[{\mathcal {E}}_{M}(t)\xi _{M}(t)]^{-1}$![]() . We see that the collapse in figure 7(b), where $s\to \infty$
. We see that the collapse in figure 7(b), where $s\to \infty$![]() , is much better than that in figure 7(a), where $s=1$
, is much better than that in figure 7(a), where $s=1$![]() , and it is almost as good as that in figure 7(c), where the actual values of $\xi _{M}(t)$
, and it is almost as good as that in figure 7(c), where the actual values of $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() are used. This supports our finding that in the fractionally helical case, the magnetic energy and correlation length are approximately given by the maximum of the values for the purely helical and purely non-helical cases, and not by their sum, as might naively have been expected.
are used. This supports our finding that in the fractionally helical case, the magnetic energy and correlation length are approximately given by the maximum of the values for the purely helical and purely non-helical cases, and not by their sum, as might naively have been expected.

Figure 7. Magnetic energy spectra similar to figure 4, but the abscissa is scaled with $\xi _{M}(t)$![]() and the ordinate with $[{\mathcal {E}}_{M}(t)\xi _{M}(t)]^{-1}$
and the ordinate with $[{\mathcal {E}}_{M}(t)\xi _{M}(t)]^{-1}$![]() , where (3.6) and (3.7) are used with $s=1$
, where (3.6) and (3.7) are used with $s=1$![]() in (a) and with $s\to \infty$
in (a) and with $s\to \infty$![]() in (b). In (c), the actual values of $\xi _{M}(t)$
in (b). In (c), the actual values of $\xi _{M}(t)$![]() and ${\mathcal {E}}_{M}(t)$
and ${\mathcal {E}}_{M}(t)$![]() are used. The last time is shown as a thick red line.
are used. The last time is shown as a thick red line.
As alluded to in § 3.3, there is a change in the shape of the spectrum as the system becomes fully helical. In particular, the position of the peak appears for slightly larger values of $k\xi _{M}(t)$![]() at later times; see figure 7(c). Thus, the value of $\xi _{M}(t)$
at later times; see figure 7(c). Thus, the value of $\xi _{M}(t)$![]() is slightly overestimated, which would explain the smaller value of $t_\xi$
is slightly overestimated, which would explain the smaller value of $t_\xi$![]() compared with $t_{\mathcal {E}}$
compared with $t_{\mathcal {E}}$![]() .
.
3.5 Comparison with earlier work
As mentioned in the introduction, the switchover time from non-helically to helically dominated decay has been studied by Tevzadze et al. (Reference Tevzadze, Kisslinger, Brandenburg and Kahniashvili2012) under the assumption that $p=1$![]() and $q=1/2$
and $q=1/2$![]() (Christensson et al. Reference Christensson, Hindmarsh and Brandenburg2001) instead of $p=10/9$
(Christensson et al. Reference Christensson, Hindmarsh and Brandenburg2001) instead of $p=10/9$![]() and $q=4/9$
and $q=4/9$![]() , as now motivated by the conservation of the Hosking integral. The basic idea is to assume that at the time of switchover, $t_\ast$
, as now motivated by the conservation of the Hosking integral. The basic idea is to assume that at the time of switchover, $t_\ast$![]() , the real-space realizability condition (Biskamp Reference Biskamp2003; Kahniashvili et al. Reference Kahniashvili, Brandenburg, Tevzadze and Ratra2010) is saturated, i.e. $2\xi _{M}(t_\ast ){\mathcal {E}}_{M}(t_\ast )/\rho _0=I_{M}$
, the real-space realizability condition (Biskamp Reference Biskamp2003; Kahniashvili et al. Reference Kahniashvili, Brandenburg, Tevzadze and Ratra2010) is saturated, i.e. $2\xi _{M}(t_\ast ){\mathcal {E}}_{M}(t_\ast )/\rho _0=I_{M}$![]() . Next, inserting $\xi _{M}(t_\ast )=\xi _{M}(t_0)\,(t_\ast /t_0)^q$
. Next, inserting $\xi _{M}(t_\ast )=\xi _{M}(t_0)\,(t_\ast /t_0)^q$![]() and ${\mathcal {E}}_{M}(t_\ast )={\mathcal {E}}_{M}(t_0)\,(t_\ast /t_0)^{-p}$
and ${\mathcal {E}}_{M}(t_\ast )={\mathcal {E}}_{M}(t_0)\,(t_\ast /t_0)^{-p}$![]() , we find $2\xi _{M}(t_0){\mathcal {E}}_{M}(t_0)/\rho _0\,(t_\ast /t_0)^{-(p-q)}=I_{M}$
, we find $2\xi _{M}(t_0){\mathcal {E}}_{M}(t_0)/\rho _0\,(t_\ast /t_0)^{-(p-q)}=I_{M}$![]() , and therefore
, and therefore
For $p=1$![]() and $q=1/2$
and $q=1/2$![]() , we have $1/(p-q)=2$
, we have $1/(p-q)=2$![]() and recover the result of Tevzadze et al. (Reference Tevzadze, Kisslinger, Brandenburg and Kahniashvili2012), while for $p=10/9$
and recover the result of Tevzadze et al. (Reference Tevzadze, Kisslinger, Brandenburg and Kahniashvili2012), while for $p=10/9$![]() and $q=4/9$
and $q=4/9$![]() , we have $1/(p-q)=3/2$
, we have $1/(p-q)=3/2$![]() . Comparing with (3.11), we see that $I_{M}$
. Comparing with (3.11), we see that $I_{M}$![]() enters with the same exponent $3/2$
enters with the same exponent $3/2$![]() , and that the remainder can be identified with
, and that the remainder can be identified with
This suggests that $I_{H}$![]() is related to $\xi _{M}$
is related to $\xi _{M}$![]() and ${\mathcal {E}}_{M}$
and ${\mathcal {E}}_{M}$![]() , but the problem is that $t_0$
, but the problem is that $t_0$![]() is not straightforwardly related to the Alfvén time $\xi _{M}/v_{A}$
is not straightforwardly related to the Alfvén time $\xi _{M}/v_{A}$![]() , where $v_{A}^2=2{\mathcal {E}}_{M}/\rho _0$
, where $v_{A}^2=2{\mathcal {E}}_{M}/\rho _0$![]() . Indeed, Brandenburg, Neronov & Vazza (Reference Brandenburg, Neronov and Vazza2024) found that there is a pre-factor $C_{M}$
. Indeed, Brandenburg, Neronov & Vazza (Reference Brandenburg, Neronov and Vazza2024) found that there is a pre-factor $C_{M}$![]() that increases with increasing magnetic Reynolds number. Such a factor has been motivated based on magnetic reconnection arguments (Hosking & Schekochihin Reference Hosking and Schekochihin2023a). Thus, inserting $t=C_{M}\xi _{M}/v_{A}$
that increases with increasing magnetic Reynolds number. Such a factor has been motivated based on magnetic reconnection arguments (Hosking & Schekochihin Reference Hosking and Schekochihin2023a). Thus, inserting $t=C_{M}\xi _{M}/v_{A}$![]() , we find
, we find
The fact that $C_{M}$![]() enters quadratically and approaches values in the range 20–50 for large magnetic Reynolds numbers explains why $I_{H}$
enters quadratically and approaches values in the range 20–50 for large magnetic Reynolds numbers explains why $I_{H}$![]() strongly exceeds the naive estimate $\xi _{M}^5v_{A}^4$
strongly exceeds the naive estimate $\xi _{M}^5v_{A}^4$![]() . Interestingly, Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) found that part of the large excess over the naive estimate is related to non-Gaussianity. Another smaller part has to do with the spectral shape. Linking the value of $C_{M}$
. Interestingly, Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) found that part of the large excess over the naive estimate is related to non-Gaussianity. Another smaller part has to do with the spectral shape. Linking the value of $C_{M}$![]() to non-Gaussianity of the magnetic field provides a new clue to the question of why there is a resistivity-dependent relation between decay and Alfvén times in hydromagnetic turbulence.
to non-Gaussianity of the magnetic field provides a new clue to the question of why there is a resistivity-dependent relation between decay and Alfvén times in hydromagnetic turbulence.
3.6 Can the switchover time be resistively limited?
We know that the decay time, $\tau (t)=(-{\rm d} {}\ln {\mathcal {E}}_{M}/{\rm d} {} t)^{-1}=t/p(t)$![]() , can be regarded as resistively limited when relating it to the Alfvén time, $\tau _{A}=\xi _{M}/v_{A}$
, can be regarded as resistively limited when relating it to the Alfvén time, $\tau _{A}=\xi _{M}/v_{A}$![]() . In particular, as alluded to in § 3.5, it turns out that $\tau /\tau _{A}=C_{M}( {\textit {Lu}})$
. In particular, as alluded to in § 3.5, it turns out that $\tau /\tau _{A}=C_{M}( {\textit {Lu}})$![]() , which is a monotonically increasing function of ${\textit {Lu}}$
, which is a monotonically increasing function of ${\textit {Lu}}$![]() that saturates near ${\textit {Lu}}_\ast$
that saturates near ${\textit {Lu}}_\ast$![]() at $C_{M}^\ast \approx 50$
at $C_{M}^\ast \approx 50$![]() (Brandenburg et al. Reference Brandenburg, Neronov and Vazza2024). Such a relation was theoretically expected and has been associated with magnetic reconnection (Hosking & Schekochihin Reference Hosking and Schekochihin2023a). However $C_{M}( {\textit {Lu}})$
(Brandenburg et al. Reference Brandenburg, Neronov and Vazza2024). Such a relation was theoretically expected and has been associated with magnetic reconnection (Hosking & Schekochihin Reference Hosking and Schekochihin2023a). However $C_{M}( {\textit {Lu}})$![]() was found to be independent of the value of the magnetic Prandtl number, which raised doubts about this interpretation.
was found to be independent of the value of the magnetic Prandtl number, which raised doubts about this interpretation.
The question now is whether the switchover time might also depend on the value of ${\textit {Lu}}$![]() . Differentiating (3.7) or (3.9), we see that the decay time depends on whether $t< t_\ast$
. Differentiating (3.7) or (3.9), we see that the decay time depends on whether $t< t_\ast$![]() or $t>t_\ast$
or $t>t_\ast$![]() and is equal to $9t/10$
and is equal to $9t/10$![]() or $3t/2$
or $3t/2$![]() , respectively, but the switchover time itself is unaffected by resistivity effects. In other words, the decay time is always $t/p$
, respectively, but the switchover time itself is unaffected by resistivity effects. In other words, the decay time is always $t/p$![]() , where the value of $p$
, where the value of $p$![]() depends on the time.
depends on the time.
There is also the possibility that for ${\textit {Lu}}< {\textit {Lu}}_\ast$![]() , the exponent $p$
, the exponent $p$![]() might depend on the order of the diffusion operator, i.e. on whether it is proportional to $\nabla ^2$
might depend on the order of the diffusion operator, i.e. on whether it is proportional to $\nabla ^2$![]() or some higher power; see Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for details. However, this consideration only applies to the regime of low enough values of ${\textit {Lu}}$
or some higher power; see Zhou et al. (Reference Zhou, Sharma and Brandenburg2022) for details. However, this consideration only applies to the regime of low enough values of ${\textit {Lu}}$![]() and it would still not affect the actual value of $t_\ast$
and it would still not affect the actual value of $t_\ast$![]() .
.
3.7 Hosking scaling at intermediate length scales
Hosking & Schekochihin (Reference Hosking and Schekochihin2021) presented arguments that for finite magnetic helicity, the Hosking scaling should only be obeyed at intermediate length scales. To check this, we now use the box-counting method as described by (2.7) to plot $\mathcal {I}_{H}(t,R)$![]() at different times $t$
at different times $t$![]() . The result is shown in figure 8 and resembles the sketch provided in figure 10 of Hosking & Schekochihin (Reference Hosking and Schekochihin2021). We do indeed see a short plateau where the Hosking scaling can be discerned for intermediate times. Furthermore, at later times, we see the expected $R^3$
. The result is shown in figure 8 and resembles the sketch provided in figure 10 of Hosking & Schekochihin (Reference Hosking and Schekochihin2021). We do indeed see a short plateau where the Hosking scaling can be discerned for intermediate times. Furthermore, at later times, we see the expected $R^3$![]() scaling over the whole range of $R$
scaling over the whole range of $R$![]() .
.

Figure 8. Box-counting result for $\mathcal {I}_{H}(R)$![]() for runs B and C in the left- and right-hand panels. Note the plateau for intermediate values of $R$
for runs B and C in the left- and right-hand panels. Note the plateau for intermediate values of $R$![]() at early times.
at early times.
3.8 Comment on the case of a finite mean field
Our simulations presented above had zero mean field. It is well known that in the presence of a mean field across the entire domain, the magnetic helicity is no longer conserved (Berger Reference Berger1997; Brandenburg & Matthaeus Reference Brandenburg and Matthaeus2004); see Brandenburg et al. (Reference Brandenburg, Durrer, Huang, Kahniashvili, Mandal and Mukohyama2020) for corresponding decay simulations in the presence of a mean field. To check whether the Hosking integral could still be meaningful in such a case, we now present the time dependence of $I_{H}(t)$![]() for Run D with different magnetic field strength, where a mean field $\boldsymbol {B}_{m}=B_{m}\hat {\boldsymbol {x}} {}$
for Run D with different magnetic field strength, where a mean field $\boldsymbol {B}_{m}=B_{m}\hat {\boldsymbol {x}} {}$![]() is now imposed, so the magnetic field is given by $\boldsymbol {B}=\boldsymbol {B}_{m}+{\boldsymbol {\nabla }}\times \boldsymbol {A}$
is now imposed, so the magnetic field is given by $\boldsymbol {B}=\boldsymbol {B}_{m}+{\boldsymbol {\nabla }}\times \boldsymbol {A}$![]() . As before, we evaluate $I_{H}(t)=2{\rm \pi} ^2 {\rm Sp}(h)/k^2$
. As before, we evaluate $I_{H}(t)=2{\rm \pi} ^2 {\rm Sp}(h)/k^2$![]() at $k=k_1$
at $k=k_1$![]() . The result is shown in figure 9 for four values of $v_{\rm Am}$
. The result is shown in figure 9 for four values of $v_{\rm Am}$![]() . We see that $I_{H}(t)$
. We see that $I_{H}(t)$![]() is now decaying $\propto t^{-2}$
is now decaying $\propto t^{-2}$![]() , i.e. the Hosking integral is not conserved. Thus, with periodic boundary conditions, not only is $I_{M}$
, i.e. the Hosking integral is not conserved. Thus, with periodic boundary conditions, not only is $I_{M}$![]() not conserved, but $I_{H}$
not conserved, but $I_{H}$![]() is also not conserved.
is also not conserved.

Figure 9. Time dependence of ${\rm Sp}(h)$![]() for Run D (solid curve, $v_{\rm Am}/c_{s}=0.1$
for Run D (solid curve, $v_{\rm Am}/c_{s}=0.1$![]() ) and several cases with weaker mean field ($v_{\rm Am}/c_{s}=0.05$
) and several cases with weaker mean field ($v_{\rm Am}/c_{s}=0.05$![]() for the dashed-dotted line, 0.02 for the dashed line and 0.01 for the dotted line).
for the dashed-dotted line, 0.02 for the dashed line and 0.01 for the dotted line).
3.9 Comment on the case with chiral fermions
As we have mentioned in the introduction, the Hosking integral also describes the decay of helical turbulence in the presence of chiral fermions if their chirality exactly balances the magnetic helicity. One may therefore ask whether a switchover to helical scaling could also occur in this case of the initial balance being not perfect. In Brandenburg et al. (Reference Brandenburg, Kamada, Mukaida, Schmitz and Schober2023a), two cases of imbalanced chirality were presented. In the case where the magnetic helicity exceeds the negative contribution to the chirality, a helical decay scaling $\propto t^{-2/3}$![]() of the magnetic energy was found, thus supporting our expectation. In the opposite case of an excess of fermion chirality, the time evolution of the magnetic energy was more complicated and no clear scaling suggestive of a helical decay was found.
of the magnetic energy was found, thus supporting our expectation. In the opposite case of an excess of fermion chirality, the time evolution of the magnetic energy was more complicated and no clear scaling suggestive of a helical decay was found.
4 Conclusions
The present work has shown that the decay laws for the combined case of two conserved quantities are best represented not simply by the sum of the individual laws, but that a good description of the numerical results is obtained by taking the maximum between the two individual decay laws. The switchover from one to the other decay law occurs earlier for $\xi _{M}(t)$![]() than for ${\mathcal {E}}_{M}(t)$
than for ${\mathcal {E}}_{M}(t)$![]() . This behaviour is surprising, but confirmed by direct inspection of the two time traces in figures 5(b) and 5(d) and perhaps explained by changes in the shape of the magnetic energy spectrum during an otherwise almost perfectly self-similar decay.
. This behaviour is surprising, but confirmed by direct inspection of the two time traces in figures 5(b) and 5(d) and perhaps explained by changes in the shape of the magnetic energy spectrum during an otherwise almost perfectly self-similar decay.
Comparing with earlier work on the switchover from one to the other regime suggests that the ratio of the decay time to the Alfvén time enters in such a relation. This is remarkable, because in hydromagnetic turbulence the decay time is known to be longer than the Alfvén time by a resistivity-dependent factor of up to 50 (Brandenburg et al. Reference Brandenburg, Neronov and Vazza2024). This large factor might also explain why the value of the Hosking integral is always found to strongly exceed the naive estimate $\xi _{M}^5v_{A}^4$![]() . In other words, the reason why this simple formula underestimates the value of the Hosking integral might be the occurrence of the same resistivity-dependent factor that also occurs in the expression for the Alfvén time. However, as shown in Zhou et al. (Reference Zhou, Sharma and Brandenburg2022), also other factors enter that involve the spectral shape. It would therefore be interesting to revisit this question.
. In other words, the reason why this simple formula underestimates the value of the Hosking integral might be the occurrence of the same resistivity-dependent factor that also occurs in the expression for the Alfvén time. However, as shown in Zhou et al. (Reference Zhou, Sharma and Brandenburg2022), also other factors enter that involve the spectral shape. It would therefore be interesting to revisit this question.
As alluded to in the introduction, an obvious astrophysical application of our work is the decay of an initially bihelical magnetic field. Such situations are important in proto-neutron stars after the neutrino-driven convection ceases. Although this was actually our initial motivation, we have not analysed this case any further, because the most important aspect turned out to be the fact that the magnetic field has always fractional helicity in such cases, which we have now addressed in the present paper. A problem with the application to proto-neutron stars is of course the fact that in stars the magnetic field is inhomogeneous and the decay is initially not yet magnetically dominated; see Brandenburg et al. (Reference Brandenburg, Kahniashvili, Mandal, Pol Roper, Tevzadze and Vachaspati2019) and Uchida et al. (Reference Uchida, Fujiwara, Kamada and Yokoyama2024). Another obvious application is to the decay of primordial magnetic fields during the radiation-dominated era of the early universe, which led to the aforementioned work by Tevzadze et al. (Reference Tevzadze, Kisslinger, Brandenburg and Kahniashvili2012).
A more general question is that of a decay governed by two decay laws and whether there are other useful examples where the physics discussed in the present paper can be studied. As far as turbulence is concerned, one might think of the Saffman and Loitsyansky integrals, which represent the coefficients of the $k^2$![]() and $k^4$
and $k^4$![]() terms in the Taylor expansion of the kinetic energy spectrum (see e.g. Davidson Reference Davidson2000). An initial $k^4$
terms in the Taylor expansion of the kinetic energy spectrum (see e.g. Davidson Reference Davidson2000). An initial $k^4$![]() spectrum (for a vanishing Saffman integral) might survive for some time, but neither of the two integrals is well conserved, and the Saffman integral might become important at later times when long-range interactions have occurred (Hosking & Schekochihin Reference Hosking and Schekochihin2023b). This idea could also be applied to the magnetic case.
spectrum (for a vanishing Saffman integral) might survive for some time, but neither of the two integrals is well conserved, and the Saffman integral might become important at later times when long-range interactions have occurred (Hosking & Schekochihin Reference Hosking and Schekochihin2023b). This idea could also be applied to the magnetic case.
The case with an imposed magnetic field in a triply periodic domain is known to be peculiar. The mean magnetic helicity density of the remaining magnetic field (without the imposed one) is not conserved (Berger Reference Berger1997). Although one can construct an additional quantity that takes the imposed field into account (Stribling, Matthaeus & Ghosh Reference Stribling, Matthaeus and Ghosh1994), it turns out that it is not gauge-variant (Brandenburg & Matthaeus Reference Brandenburg and Matthaeus2004). Our present work has shown that with an imposed mean magnetic field, also the Hosking integral is no longer conserved and tends to zero.
In summary, the present work has extended our knowledge about the Hosking integral, a remarkably useful quantity whose influence on many aspects of decaying hydromagnetic turbulence can be understood based on dimensional analysis. Numerical simulations are used to pinpoint the values of the coefficients. For several different systems, the set of these coefficients has been found to be similar, suggesting that their values might be fundamental quantities. But more work is required to establish this more firmly.
Acknowledgements
We thank I. Khaymovich and G. Vasil for inspiring discussions and useful comments on our work. We are also grateful to the three referees for their constructive remarks that have improved the presentation of our paper.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Funding
This work was supported in part by the Swedish Research Council (Vetenskapsrådet, 2019-04234), the National Science Foundation under grant no. NSF AST-2307698 and NASA ATP Award 80NSSC22K0825. We acknowledge the inspiring atmosphere during the programme on the ‘Generation, evolution, and observations of cosmological magnetic fields’ at the Bernoulli Center in Lausanne. We acknowledge the allocation of computing resources provided by the Swedish National Allocations Committee at the Center for Parallel Computers at the Royal Institute of Technology in Stockholm and Linköping.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are openly available on Zenodo at https://doi.org/10.5281/zenodo.14028931 (v2024.11.02) or, for easier access, at http://norlx65.nordita.org/~brandenb/projects/Two-Conserved/. All calculations have been performed with the Pencil Code (Pencil Code Collaboration et al. 2021); https://doi.org/10.5281/zenodo.3961647.