Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T03:26:52.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Alfvénic turbulence in relativistic plasmas.Part 2. current sheets and dissipation

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  03 November 2021

B. Ripperda Open the ORCID record for B. Ripperda [Opens in a new window] ,
J.F. Mahlmann Open the ORCID record for J.F. Mahlmann [Opens in a new window] ,
A. Chernoglazov ,
J.M. TenBarge Open the ORCID record for J.M. TenBarge [Opens in a new window] ,
E.R. Most ,
J. Juno Open the ORCID record for J. Juno [Opens in a new window] ,
Y. Yuan Open the ORCID record for Y. Yuan [Opens in a new window] ,
A.A. Philippov  and
A. Bhattacharjee
B. Ripperda*
Affiliation:
Center for Computational Astrophysics, Flatiron Institute, 162 Fifth Avenue, New York, NY10010, USA Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ08544, USA
J.F. Mahlmann*
Affiliation:
Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ08544, USA
A. Chernoglazov
Affiliation:
Center for Computational Astrophysics, Flatiron Institute, 162 Fifth Avenue, New York, NY10010, USA Department of Physics, University of New Hampshire, 9 Library Way, Durham, NH03824, USA
J.M. TenBarge
Affiliation:
Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ08544, USA Princeton Center for Heliophysics, Princeton University, Princeton, NJ08540, USA
E.R. Most
Affiliation:
Princeton Center for Theoretical Science, Princeton University, Princeton, NJ08544, USA Princeton Gravity Initiative, Princeton University, Princeton, NJ08544, USA School of Natural Sciences, Institute for Advanced Study, Princeton, NJ08540, USA
J. Juno
Affiliation:
Department of Physics and Astronomy, University of Iowa, Iowa City, IA52242, USA
Y. Yuan
Affiliation:
Center for Computational Astrophysics, Flatiron Institute, 162 Fifth Avenue, New York, NY10010, USA
A.A. Philippov
Affiliation:
Center for Computational Astrophysics, Flatiron Institute, 162 Fifth Avenue, New York, NY10010, USA
A. Bhattacharjee
Affiliation:
Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ08544, USA Princeton Center for Heliophysics, Princeton University, Princeton, NJ08540, USA
*
†Email addresses for correspondence: bripperda@flatironinstitute.org, mahlmann@princeton.edu
†Email addresses for correspondence: bripperda@flatironinstitute.org, mahlmann@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Alfvén waves as excited in black hole accretion disks and neutron star magnetospheres are the building blocks of turbulence in relativistic, magnetized plasmas. A large reservoir of magnetic energy is available in these systems, such that the plasma can be heated significantly even in the weak turbulence regime. 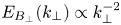We perform high-resolution three-dimensional simulations of counter-propagating Alfvén waves, showing that an $E_{B_{\perp }}(k_{\perp }) \propto k_{\perp }^{-2}$ energy spectrum develops as a result of the weak turbulence cascade in relativistic magnetohydrodynamics and its infinitely magnetized (force-free) limit. The plasma turbulence ubiquitously generates current sheets, which act as locations where magnetic energy dissipates. We show that current sheets form as a natural result of nonlinear interactions between counter-propagating Alfvén waves. These current sheets form owing to the compression of elongated eddies, driven by the shear induced by growing higher-order modes, and undergo a thinning process until they break-up into small-scale turbulent structures. We explore the formation of current sheets both in overlapping waves and in localized wave packet collisions. The relativistic interaction of localized Alfvén waves induces both Alfvén waves and fast waves, and efficiently mediates the conversion and dissipation of electromagnetic energy in astrophysical systems. Plasma energization through reconnection in current sheets emerging during the interaction of Alfvén waves can potentially explain X-ray emission in black hole accretion coronae and neutron star magnetospheres.

Keywords

MHD turbulenceturbulence simulationcomputational methodstransition to turbulence
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 5 , October 2021 , 905870512
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alic, D., Moesta, P., Rezzolla, L., Zanotti, O. & Jaramillo, J.L. 2012 Accurate simulations of binary black hole mergers in force-free electrodynamics. Astrophys. J. 754 (1), 36.CrossRefGoogle Scholar
Bhattacharjee, A., Huang, Y.-M., Yang, H. & Rogers, B. 2009 Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16 (11), 112102.CrossRefGoogle Scholar
Bhattacharjee, A. & Ng, C.S. 2001 Random scattering and anisotropic turbulence of shear alfvén wave packets. Astrophys. J. 548 (1), 318–322.CrossRefGoogle Scholar
Biskamp, D. 2000 Magnetic Reconnection in Plasmas, vol. 3. Cambridge University Press.CrossRefGoogle Scholar
Blandford, R.D. 2002 To the lighthouse. In Lighthouses of the Universe: The Most Luminous Celestial Objects and their Use for Cosmology (ed. M. Gilfanov, R. Sunyeav & E. Churazov), p. 381. Springer.Google Scholar
Blandford, R.D. & Znajek, R.L. 1977 Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 179, 433–456.CrossRefGoogle Scholar
Boldyrev, S. 2005 On the spectrum of magnetohydrodynamic turbulence. Astrophys. J. Lett. 626 (1), L37–L40.CrossRefGoogle Scholar
Boldyrev, S. 2006 Spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 96 (11), 115002.CrossRefGoogle ScholarPubMed
Bransgrove, A., Beloborodov, A.M. & Levin, Y. 2020 A quake quenching the vela pulsar. Astrophys. J. 897 (2), 173.CrossRefGoogle Scholar
Burgers, J.M. 1948 A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199. Elsevier.CrossRefGoogle Scholar
Čada, M. & Torrilhon, M. 2009 Compact third-order limiter functions for finite volume methods. J. Comput. Phys. 228, 4118.CrossRefGoogle Scholar
Chandran, B.D.G. 2005 Weak compressible magnetohydrodynamic turbulence in the solar corona. Phys. Rev. Lett. 95, 265004.CrossRefGoogle ScholarPubMed
Chandran, B.D.G., Foucart, F. & Tchekhovskoy, A. 2018 Heating of accretion-disk coronae and jets by general relativistic magnetohydrodynamic turbulence. J. Plasma Phys. 84 (3), 905840310.CrossRefGoogle Scholar
Chandran, B.D.G., Schekochihin, A.A. & Mallet, A. 2015 Intermittency and alignment in strong RMHD turbulence. Astrophys. J. 807 (1), 39.CrossRefGoogle Scholar
Chernoglazov, A., Ripperda, B. & Philippov, A. 2021 Dynamic alignment and plasmoid formation in relativistic magnetohydrodynamic turbulence. Astrophys. J. Lett. (submitted).CrossRefGoogle Scholar
Cho, J. 2005 Simulations of relativistic force-free magnetohydrodynamic turbulence. Astrophys. J. 621 (1), 324–327.CrossRefGoogle Scholar
Cho, J. & Lazarian, A. 2002 Compressible sub-alfvenic MHD turbulence in low-$\beta$ plasmas. Phys. Rev. Lett. 88 (24), 245001.CrossRefGoogle ScholarPubMed
Cho, J. & Lazarian, A. 2003 Compressible magnetohydrodynamic turbulence: mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. Mon. Not. R. Astron. Soc. 345, 325–339.CrossRefGoogle Scholar
Cho, J. & Vishniac, E.T. 2000 The anisotropy of magnetohydrodynamic alfvénic turbulence. Astrophys. J. 539 (1), 273–282.CrossRefGoogle Scholar
Comisso, L., Huang, Y.M., Lingam, M., Hirvijoki, E. & Bhattacharjee, A. 2018 Magnetohydrodynamic turbulence in the plasmoid-mediated regime. Astrophys. J. 854 (2), 103.CrossRefGoogle Scholar
Comisso, L. & Sironi, L. 2018 Particle acceleration in relativistic plasma turbulence. Phys. Rev. Lett. 121 (25), 255101.CrossRefGoogle ScholarPubMed
Del Zanna, L., Papini, E., Landi, S., Bugli, M. & Bucciantini, N. 2016 Fast reconnection in relativistic plasmas: the magnetohydrodynamics tearing instability revisited. Mon. Not. R. Astron. Soc. 460 (4), 3753–3765.CrossRefGoogle Scholar
Dong, C., Wang, L., Huang, Y., Comisso, L. & Bhattacharjee, A. 2018 Role of the plasmoid instability in magnetohydrodynamic turbulence. Phys. Rev. Lett. 121 (16), 165101.CrossRefGoogle ScholarPubMed
Duncan, R.C. & Thompson, C. 1992 Formation of very strongly magnetized neutron stars: implications for gamma-ray bursts. Astrophys. J. Lett. 392, L9.CrossRefGoogle Scholar
Evans, C.R. & Hawley, J.F. 1988 Simulation of magnetohydrodynamic flows: a constrained transport model. Astrophys. J. 332, 659.CrossRefGoogle Scholar
Farge, M. & Schneider, K. 2006 Encyclopedia of Mathematical Physics. Elsevier.Google Scholar
Galtier, S., Nazarenko, S.V., Newell, A.C. & Pouquet, A. 2000 A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63 (5), 447–488.CrossRefGoogle Scholar
Goldreich, P. & Julian, W.H. 1969 Pulsar electrodynamics. Astrophys. J. 157, 869.CrossRefGoogle Scholar
Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. II. Strong alfvenic turbulence. Astrophys. J. 438, 763.CrossRefGoogle Scholar
Gruzinov, A. 1999 Stability in force-free electrodynamics. arXiv:astro-ph/9902288.Google Scholar
Heyl, J.S. & Hernquist, L. 1999 Nonlinear QED effects in strong-field magnetohydrodynamics. Phys. Rev. D 59 (4), 045005.CrossRefGoogle Scholar
Howes, G.G. 2014 The inherently three-dimensional nature of magnetized plasma turbulence. J. Plasma Phys. 81 (2), 325810203.Google Scholar
Howes, G.G. 2016 The dynamical generation of current sheets in astrophysical plasma turbulence. Astrophys. J. 827 (2), L28.CrossRefGoogle Scholar
Howes, G.G., McCubbin, A.J. & Klein, K.G. 2018 Spatially localized particle energization by Landau damping in current sheets produced by strong alfvén wave collisions. J. Plasma Phys. 84, 905840105.CrossRefGoogle Scholar
Howes, G.G. & Nielson, K.D. 2013 Alfvén wave collisions, the fundamental building block of plasma turbulence. I. Asymptotic solution. Phys. Plasmas 20 (7), 072302.CrossRefGoogle Scholar
Huang, Y.M. & Bhattacharjee, A. 2016 Turbulent magnetohydrodynamic reconnection mediated by the plasmoid instability. Astrophys. J. 818 (1), 20.CrossRefGoogle Scholar
Komissarov, S.S., Barkov, M. & Lyutikov, M. 2007 Tearing instability in relativistic magnetically dominated plasmas. Mon. Not. R. Astron. Soc. 374 (2), 415–426.CrossRefGoogle Scholar
Kuznetsov, E.A. 2001 Weak magnetohydrodynamic turbulence of a magnetized plasma. J. Expl Theor. Phys. 93 (5), 1052–1064.CrossRefGoogle Scholar
Li, X. & Beloborodov, A.M. 2015 Plastic damping of alfvén waves in magnetar flares and delayed afterglow emission. Astrophys. J. 815 (1), 25.CrossRefGoogle Scholar
Li, X., Beloborodov, A.M. & Sironi, L. 2021 Fast dissipation of colliding alfvén waves in a magnetically dominated plasma. arXiv:2103.05700.CrossRefGoogle Scholar
Li, X., Zrake, J. & Beloborodov, A.M. 2019 Dissipation of alfvén waves in relativistic magnetospheres of magnetars. Astrophys. J. 881 (1), 13.CrossRefGoogle Scholar
Londrillo, P. & del Zanna, L. 2004 On the divergence-free condition in Godunov-type schemes for ideal magnetohydrodynamics: the upwind constrained transport method. J. Comput. Phys. 195 (1), 17–48.CrossRefGoogle Scholar
Loureiro, N.F. & Boldyrev, S. 2017 Role of magnetic reconnection in magnetohydrodynamic turbulence. Phys. Rev. Lett. 118 (24), 245101.CrossRefGoogle ScholarPubMed
Mahlmann, J.F. 2020 Dynamics in the magnetospheres of compact objects. PhD thesis, Universitat de València.Google Scholar
Mahlmann, J.F., Aloy, M.A., Mewes, V. & Cerdá-Durán, P. 2021 a Computational general relativistic force-free electrodynamics. I. Multi-coordinate implementation and testing. Astron. Astrophys. 647, A57.CrossRefGoogle Scholar
Mahlmann, J.F., Aloy, M.A., Mewes, V. & Cerdá-Durán, P. 2021 b Computational general relativistic force-free electrodynamics. II. Characterization of numerical diffusivity. Astron. Astrophys. 647, A58.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A. & Chandran, B.D.G. 2015 Refined critical balance in strong Alfvénic turbulence. Mon. Not. R. Astron. Soc. 449, L77–L81.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A. & Chandran, B.D.G. 2017 Disruption of Alfvénic turbulence by magnetic reconnection in a collisionless plasma. J. Plasma Phys. 83 (6), 905830609.CrossRefGoogle Scholar
Maron, J. & Goldreich, P. 2001 Simulations of incompressible magnetohydrodynamic turbulence. Astrophys. J. 554, 1175–1196.CrossRefGoogle Scholar
Matthaeus, W.H. & Lamkin, S.L. 1986 Turbulent magnetic reconnection. Phys. Fluids 29, 2513–2534.CrossRefGoogle Scholar
Media Supplement A 2021 Interaction of continuously overlapping alfvén waves: 2d current and field structure. https://youtu.be/HHacblwqiS0. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement B 2021 Interaction of continuously overlapping alfvén waves: 3d current structure. https://youtu.be/GTLvtH7CKOs. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement C 2021 Interaction of alfvén wave packets: 2d growth and dynamics of the $(1, 1)$ mode. https://youtu.be/Rd9qTNyaN5s. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement D 2021 Interaction of alfvén wave packets: 2d current and field structure for the $\mathrm {AW}_3+\mathrm {AW}_3$ setup. https://youtu.be/E3wjj4blpg8. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement E 2021 Interaction of alfvén wave packets: 2d current and field structure for the $\mathrm {AW}_1+\mathrm {AW}_3$ setup. https://youtu.be/iEIlV3q1Oto, The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement F 2021 Interaction of alfvén wave packets: 3d current structure for the $\mathrm {AW}_3+\mathrm {AW}_3$ setup. https://youtu.be/EMBVLRTtaHg. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement G 2021 Interaction of alfvén wave packets: 3d current structure for the $\mathrm {AW}_1+\mathrm {AW}_3$ setup. https://youtu.be/Kdmz6ebLPiQ. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Media Supplement H 2021 Interaction of alfvén wave packets: 3d growth and dynamics of the $(1, 1)$ mode. https://youtu.be/5RLFXu0D1Ps. The supplementary material was published on behalf of the authors of this manuscript.Google Scholar
Meyrand, R., Galtier, S. & Kiyani, K.H. 2016 Direct evidence of the transition from weak to strong magnetohydrodynamic turbulence. Phys. Rev. Lett. 116 (10), 105002.CrossRefGoogle ScholarPubMed
Monin, A.S. & Yaglom, A.M. 1999 Statistical fluid mechanics: the mechanics of turbulence. https://mitpress.mit.edu/books/statistical-fluid-mechanics-volume-1.CrossRefGoogle Scholar
Montgomery, D. & Matthaeus, W.H. 1995 Anisotropic modal energy transfer in interstellar turbulence. Astrophys. J. 447, 706.CrossRefGoogle Scholar
Nathanail, A., Fromm, C.M, Porth, O., Olivares, H., Younsi, Z., Mizuno, Y. & Rezzolla, L. 2020 Plasmoid formation in global GRMHD simulations and AGN flares. Mon. Not. R. Astron. Soc. 495 (2), 1549–1565.CrossRefGoogle Scholar
Nättilä, J. & Beloborodov, A.M. 2020 Radiative turbulent flares in magnetically-dominated plasmas. arXiv:2012.03043.CrossRefGoogle Scholar
Ng, C.S. & Bhattacharjee, A. 1996 Interaction of shear-alfven wave packets: implication for weak magnetohydrodynamic turbulence in astrophysical plasmas. Astrophys. J. 465, 845.CrossRefGoogle Scholar
Ng, C.S. & Bhattacharjee, A. 1997 Scaling of anisotropic spectra due to the weak interaction of shear-Alfvén wave packets. Phys. Plasmas 4 (3), 605–610.CrossRefGoogle Scholar
Nielson, K.D., Howes, G.G. & Dorland, W. 2013 Alfvén wave collisions, the fundamental building block of plasma turbulence. II. Numerical solution. Phys. Plasmas 20 (7), 072303.CrossRefGoogle Scholar
Ni, L., Germaschewski, K., Huang, Y.M., Sullivan, B.P., Yang, H. & Bhattacharjee, A. 2010 Linear plasmoid instability of thin current sheets with shear flow. Phys. Plasmas 17 (5), 052109.CrossRefGoogle Scholar
Noble, S.C., Gammie, C.F., McKinney, J.C. & Del Zanna, L. 2006 Primitive variable solvers for conservative general relativistic magnetohydrodynamics. Astrophys. J. 641 (1), 626–637.CrossRefGoogle Scholar
Olivares, H., Porth, O., Davelaar, J., Most, E.R., Fromm, C.M., Mizuno, Y., Younsi, Z. & Rezzolla, L. 2019 Constrained transport and adaptive mesh refinement in the black hole accretion code. Astron. Astrophys. 629, A61.CrossRefGoogle Scholar
Pareschi, L. & Russo, G. 2005 Implicit–explicit Runge–Kutta schemes and applications to hyperbolic systems with relaxation. J. Sci. Comput. 25 (1), 129–155.Google Scholar
Perez, J.C. & Boldyrev, S. 2008 On weak and strong magnetohydrodynamic turbulence. Astrophys. J. Lett. 672 (1), L61.CrossRefGoogle Scholar
Porth, O., Olivares, H., Mizuno, Y., Younsi, Z., Rezzolla, L., Moscibrodzka, M., Falcke, H. & Kramer, M. 2017 The black hole accretion code. Comput. Astrophys. Cosmol. 4, 1.CrossRefGoogle Scholar
Ripperda, B., Bacchini, F. & Philippov, A.A. 2020 Magnetic reconnection and hot spot formation in black hole accretion disks. Astrophys. J. 900 (2), 100.CrossRefGoogle Scholar
Ripperda, B., Bacchini, F., Porth, O., Most, E.R., Olivares, H., Nathanail, A., Rezzolla, L., Teunissen, J. & Keppens, R. 2019 a General-relativistic resistive magnetohydrodynamics with robust primitive-variable recovery for accretion disk simulations. Astrophys. J. Suppl. 244 (1), 10.CrossRefGoogle Scholar
Ripperda, B., Bacchini, F., Teunissen, J., Xia, C., Porth, O., Sironi, L., Lapenta, G. & Keppens, R. 2018 A comprehensive comparison of relativistic particle integrators. Astrophys. J. Suppl. 235 (1), 21.CrossRefGoogle Scholar
Ripperda, B., Porth, O., Sironi, L. & Keppens, R. 2019 b Relativistic resistive magnetohydrodynamic reconnection and plasmoid formation in merging flux tubes. Mon. Not. R. Astron. Soc. 485 (1), 299–314.CrossRefGoogle Scholar
Ripperda, B., Porth, O., Xia, C. & Keppens, R. 2017 a Reconnection and particle acceleration in interacting flux ropes II. 3d effects on test particles in magnetically dominated plasmas. Mon. Not. R. Astron. Soc. 471 (3), 3465–3482.CrossRefGoogle Scholar
Ripperda, B., Porth, O., Xia, C. & Keppens, R. 2017 b Reconnection and particle acceleration in interacting flux ropes I. Magnetohydrodynamics and test particles in 2.5d. Mon. Not. R. Astron. Soc. 3279–3298.Google Scholar
Rueda, J.A.A., Verscharen, D., Wicks, R.T., Owen, C.J., Nicolaou, G., Walsh, A.P., Zouganelis, I., Germaschewski, K. & Vargas Domínguez, S. 2021 Three-dimensional magnetic reconnection in particle-in-cell simulations of anisotropic plasma turbulence. arXiv:2103.13232.Google Scholar
Rusanov, V.V. 1961 Calculation of interaction of non–steady shock waves with obstacles. J. Comput. Math. Phys. USSR 1, 267–279.Google Scholar
Schekochihin, A.A., Nazarenko, S.V. & Yousef, T.A. 2012 Weak Alfvén-wave turbulence revisited. Phys. Rev. E 85 (3), 036406.CrossRefGoogle ScholarPubMed
Sonnerup, B.U.O. & Cahill, L.J.Jr. 1967 Magnetopause structure and attitude from explorer 12 observations. J. Geophys. Res. 72, 171.CrossRefGoogle Scholar
Sridhar, S. & Goldreich, P. 1994 Toward a theory of interstellar turbulence. I. Weak alfvenic turbulence. Astrophys. J. 432, 612.CrossRefGoogle Scholar
Suresh, A. & Huynh, H.T. 1997 Accurate monotonicity-preserving schemes with Runge–Kutta time stepping. J. Comput. Phys. 136 (1), 83–99.CrossRefGoogle Scholar
Takamoto, M. & Lazarian, A. 2017 Strong coupling of alfvén and fast modes in compressible relativistic magnetohydrodynamic turbulence in magnetically dominated plasmas. Mon. Not. R. Astron. Soc. 472 (4), 4542–4550.CrossRefGoogle Scholar
TenBarge, J.M. & Howes, G.G. 2013 Current sheets and collisionless damping in kinetic plasma turbulence. Astrophys. J. 771 (2), L27.CrossRefGoogle Scholar
TenBarge, J.M., Ripperda, B., Chernoglazov, A., Bhattacharjee, A., Mahlmann, J.F., Most, E.R., Juno, J., Yuan, Y. & Philippov, A.A. 2021 Weak alfvénic turbulence in relativistic magnetically dominated plasmas I: asymptotic solutions. J. Plasma Phys. (submitted).Google Scholar
Thompson, C. & Blaes, O. 1998 Magnetohydrodynamics in the extreme relativistic limit. Phys. Rev. D 57, 3219–3234.CrossRefGoogle Scholar
Troischt, P. & Thompson, C. 2004 Force-free magnetohydrodynamic waves: nonlinear interactions and effects of strong gravity. Phys. Rev. D 70 (12), 124030.CrossRefGoogle Scholar
Uzdensky, D.A., Loureiro, N.F. & Schekochihin, A.A. 2010 Fast magnetic reconnection in the plasmoid-dominated regime. Phys. Rev. Lett. 105, 23.CrossRefGoogle ScholarPubMed
Verdini, A. & Grappin, R. 2012 Transition from weak to strong cascade in MHD turbulence. Phys. Rev. Lett. 109 (2), 025004.CrossRefGoogle ScholarPubMed
Verniero, J.L. & Howes, G.G. 2018 The alfvénic nature of energy transfer mediation in localized, strongly nonlinear alfvén wavepacket collisions. J. Plasma Phys. 84, 905840109.Google Scholar
Verniero, J.L., Howes, G.G. & Klein, K.G. 2018 Nonlinear energy transfer and current sheet development in localized alfvén wavepacket collisions in the strong turbulence limit. J. Plasma Phys. 84, 905840103.Google Scholar
Werner, G.R. & Uzdensky, D.A. 2017 Nonthermal particle acceleration in 3d relativistic magnetic reconnection in pair plasma. Astrophys. J. 843 (2), L27.CrossRefGoogle Scholar
Yuan, Y., Beloborodov, A.M., Chen, A.Y. & Levin, Y. 2020 a Plasmoid ejection by alfvén waves and the fast radio bursts from SGR $1935+2154$. Astrophys. J. 900 (2), L21.CrossRefGoogle Scholar
Yuan, Y., Levin, Y., Bransgrove, A. & Philippov, A.A. 2020 b Alfvén wave mode conversion in pulsar magnetospheres. arXiv:2007.11504.CrossRefGoogle Scholar
Zhdankin, V., Uzdensky, D.A., Perez, J.C. & Boldyrev, S. 2013 Statistical analysis of current sheets in three-dimensional magnetohydrodynamic turbulence. Astrophys. J. 771 (2), 124.CrossRefGoogle Scholar
Zhdankin, V., Uzdensky, D.A., Werner, G.R & Begelman, M.C. 2017 Numerical investigation of kinetic turbulence in relativistic pair plasmas I. Turbulence statistics. Mon. Not. R. Astron. Soc. 474 (2), 2514–2535.CrossRefGoogle Scholar