No CrossRef data available.
Article contents
ℵ0-categorical structures with arbitrarily fast growth of algebraic closure
Published online by Cambridge University Press: 12 March 2014
Extract
Various results have been proved about growth rates of certain sequences of integers associated with infinite permutation groups. Most of these concern the number of orbits of the automorphism group of an ℵ0-categorical structure 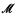 on the set of unordered n-subsets or on the set of n-tuples of elements of
on the set of unordered n-subsets or on the set of n-tuples of elements of 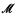 . (Recall that by the Ryll-Nardzewski Theorem, if
. (Recall that by the Ryll-Nardzewski Theorem, if 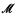 is countable and ℵ0-categorical, the number of the orbits of its automorphism group Aut(
is countable and ℵ0-categorical, the number of the orbits of its automorphism group Aut(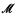 ) on the set of n-tuples from
) on the set of n-tuples from 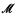 is finite and equals the number of complete n-types consistent with the theory of
is finite and equals the number of complete n-types consistent with the theory of 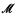 .) The book [Ca90] is a convenient reference for these results. One of the oldest (in the realms of ‘folklore’) is that for any sequence (Kn)n∈ℕ of natural numbers there is a countable ℵ0-categorical structure
.) The book [Ca90] is a convenient reference for these results. One of the oldest (in the realms of ‘folklore’) is that for any sequence (Kn)n∈ℕ of natural numbers there is a countable ℵ0-categorical structure 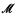 such that the number of orbits of Aut(
such that the number of orbits of Aut(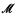 ) on the set of n-tuples from
) on the set of n-tuples from 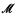 is greater than kn for all n.
is greater than kn for all n.
These investigations suggested the study of the growth rate of another sequence. Let 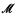 be an ℵ0-categorical structure and X be a finite subset of
be an ℵ0-categorical structure and X be a finite subset of 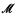 . Let acl(X) be the algebraic closure of X, that is, the union of the finite X-definable subsets of
. Let acl(X) be the algebraic closure of X, that is, the union of the finite X-definable subsets of 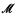 . Equivalently, this is the union of the finite orbits on
. Equivalently, this is the union of the finite orbits on 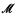 of Aut(
of Aut(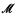 )(X), the pointwise stabiliser of X in Aut(
)(X), the pointwise stabiliser of X in Aut(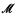 ). Define
). Define
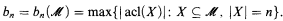
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002

