Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-24T23:15:43.921Z Has data issue: false hasContentIssue false
  • English
  • Français

$[0,n]\cup \{\omega \}$ IS A SPECTRUM OF A NON-DISINTEGRATED FLAT STRONGLY MINIMAL MODEL COMPLETE THEORY IN A LANGUAGE WITH FINITE SIGNATURE

Part of: Model theory

Published online by Cambridge University Press:  01 February 2021

URI ANDREWS  and
OMER MERMELSTEIN
URI ANDREWS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN–MADISON 480 LINCOLN DR. MADISON, WI 35706, USA E-mail: andrews@math.wisc.edu E-mail: omer@math.wisc.edu
OMER MERMELSTEIN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN–MADISON 480 LINCOLN DR. MADISON, WI 35706, USA E-mail: andrews@math.wisc.edu E-mail: omer@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We build a new spectrum of recursive models (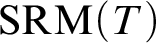$ \operatorname {\mathrm {SRM}}(T)$) of a strongly minimal theory. This theory is non-disintegrated, flat, model complete, and in a language with a finite signature.

Keywords

spectrum of recursive modelsspectrum of computable modelsflatnessHrushovski construction

MSC classification

Primary: 03C57: Effective and recursion-theoretic model theory
Secondary: 03C30: Other model constructions

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1632 - 1656
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrews, U. and Knight, J.F., Strongly minimal theories with recursive models . Journal of the European Mathematical Society, vol. 20 (2018), no. 7, pp. 1561–1594.10.4171/JEMS/793CrossRefGoogle Scholar
Andrews, U., Lempp, S., and Schweber, N., Building models of strongly minimal theories. Advances in Mathematics, vol. 386 (2021), p. 107802.CrossRefGoogle Scholar
Andrews, U. and Medvedev, A., Recursive spectra of strongly minimal theories satisfying the Zilber trichotomy. Transactions of the American Mathematical Society, vol. 366 (2014), no. 5, pp. 2393–2417.10.1090/S0002-9947-2014-05897-2CrossRefGoogle Scholar
Andrews, U., Amalgamation constructions and recursive model theory. Ph.D. thesis, University of California, Berkeley, 2010.Google Scholar
Andrews, U., New spectra of strongly minimal theories in finite languages. Annals of Pure and Applied Logic, vol. 162 (2011), no. 5, pp. 367–372.10.1016/j.apal.2010.11.002CrossRefGoogle Scholar
Andrews, U., A new spectrum of recursive models using an amalgamation construction, this Journal, vol. 76 (2011), no. 3, pp. 883–896.Google Scholar
Baldwin, J.T. and Lachlan, A.H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
Gončarov, S.S., Constructive models of ${\aleph}_1$ -categorical theories. Matematicheskie Zametki, vol. 23 (1978), no. 6, pp. 885–888.Google Scholar
Goncharov, S.S., Harizanov, V.S., Laskowski, M.C., Lempp, S., and McCoy, C.F.D., Trivial, strongly minimal theories are model complete after naming constants. Proceedings of the American Mathematical Society, vol. 131 (2003), no. 12, pp. 3901–3912.CrossRefGoogle Scholar
Hirschfeldt, D.R., Khoussainov, B., and Semukhin, P., An uncountably categorical theory whose only computably presentable model is saturated . Notre Dame Journal of Formal Logic, vol. 47 (2006), no. 1, pp. 63–71.Google Scholar
Herwig, B., Lempp, S., and Ziegler, M., Constructive models of uncountably categorical theories. Proceedings of the American Mathematical Society, vol. 127 (1999), no. 12, pp. 3711–3719.10.1090/S0002-9939-99-04920-5CrossRefGoogle Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.10.1017/CBO9780511551574CrossRefGoogle Scholar
Hrushovski, E., A new strongly minimal set. Annals Pure and Applied Logic, vol. 62 (1993), no. 2, pp. 147–166. Stability in model theory, III (Trento, 1991).10.1016/0168-0072(93)90171-9CrossRefGoogle Scholar
Khoussainov, B.M., Laskowski, M.C., Lempp, S., and Solomon, R., On the computability-theoretic complexity of trivial, strongly minimal models. Proceedings of the American Mathematical Society, vol. 135 (2007), no. 11, pp. 3711–3721.10.1090/S0002-9939-07-08865-XCrossRefGoogle Scholar
Khoussainov, B., Nies, A., and Shore, R.A., Computable models of theories with few models. Notre Dame Journal of Formal Logic, vol. 38 (1997), no. 2, pp. 165–178.10.1305/ndjfl/1039724885CrossRefGoogle Scholar
Khoussainov, B., Semukhin, P., and Stephan, F., Applications of Kolmogorov complexity to computable model theory, this Journal, vol. 72 (2007), no. 3, pp. 1041–1054.Google Scholar
Kudaĭbergenov, K.Ž., Constructivizable models of undecidable theories. Sibirskii Matematicheskii Zhurnal, vol. 21 (1980), no. 5, pp. 155–158, 192.Google Scholar
Nies, A., A new spectrum of recursive models. Notre Dame Journal of Formal Logic, vol. 40 (1999), no. 3, pp. 307–314.10.1305/ndjfl/1022615611CrossRefGoogle Scholar