Article contents
Σ1 compactness for next admissible sets1
Published online by Cambridge University Press: 12 March 2014
Extract
Let σ be any sequence B0, B1 …, Bn, … of transitive sets closed under pairs with 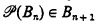 for each n. In this paper we show that the smallest admissible set Aσ with σ ∈ Aσ is Σ1 compact. Thus we have an entirely new class of explicitly describable uncountable Σ1 compact sets.
for each n. In this paper we show that the smallest admissible set Aσ with σ ∈ Aσ is Σ1 compact. Thus we have an entirely new class of explicitly describable uncountable Σ1 compact sets.
The search for uncountable Σ1 compact languages goes back to Hanf's negative results on compact cardinals [7]. Barwise first showed that all countable admissible sets were Σ1 compact [1] and then went on to give a characterization of the Σ1 compact sets in terms of strict 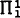 reflection [2]. While his characterization has been of interest in understanding the Σ1 compactness phenomenon it has led to the identification of only one class of uncountable Σ1 compact sets. In particular, Barwise showed [2], using the above notation, that if ⋃nBn is power set admissible it satisfies the strict
reflection [2]. While his characterization has been of interest in understanding the Σ1 compactness phenomenon it has led to the identification of only one class of uncountable Σ1 compact sets. In particular, Barwise showed [2], using the above notation, that if ⋃nBn is power set admissible it satisfies the strict 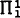 reflection principle and hence is Σ1 compact. (This result was obtained independently by Karp using algebraic methods [9].)
reflection principle and hence is Σ1 compact. (This result was obtained independently by Karp using algebraic methods [9].)
In proving our compactness theorem we follow Makkai's approach to the Barwise Compactness Theorem [12] and use a modified version of Smullyan's abstract consistency property [14]. A direct generalization of Makkai's method to the cofinality ω case yields a proof of the Barwise-Karp result mentioned above [6]. In order to obtain our new result we depart from the usual definition of language and use instead the indexed languages of Karp [9] in which a conjunction is considered to operate on a function whose range is a set of formulas rather than on a set of formulas itself.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
Footnotes
To the memory of Carol Karp, who I hope understood the depth of my gratitude.
References
REFERENCES
- 6
- Cited by

