Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:25:31.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Σ1(κ)-DEFINABLE SUBSETS OF H(κ+)

Published online by Cambridge University Press:  08 September 2017

PHILIPP LÜCKE ,
RALF SCHINDLER  and
PHILIPP SCHLICHT
PHILIPP LÜCKE
Affiliation:
MATHEMATISCHES INSTITUT, UNIVERSITÄT BONN ENDENICHER ALLEE 60 53115 BONN, GERMANY E-mail: pluecke@math.uni-bonn.de
RALF SCHINDLER
Affiliation:
INSTITUT FÜR MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG UNIVERSITÄT MÜNSTER, EINSTEINSTR. 62 48149 MÜNSTER, GERMANY E-mail: rds@math.uni-muenster.de
PHILIPP SCHLICHT
Affiliation:
MATHEMATISCHES INSTITUT, UNIVERSITÄT BONN ENDENICHER ALLEE 60 53115 BONN, GERMANY E-mail: schlicht@math.uni-bonn.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We study Σ1(ω1)-definable sets (i.e., sets that are equal to the collection of all sets satisfying a certain Σ1-formula with parameter ω1 ) in the presence of large cardinals. Our results show that the existence of a Woodin cardinal and a measurable cardinal above it imply that no well-ordering of the reals is Σ1(ω1)-definable, the set of all stationary subsets of ω1 is not Σ1(ω1)-definable and the complement of every Σ1(ω1)-definable Bernstein subset of 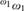${}_{}^{{\omega _1}}\omega _1^{}$ is not Σ1(ω1)-definable. In contrast, we show that the existence of a Woodin cardinal is compatible with the existence of a Σ1(ω1)-definable well-ordering of H(ω2) and the existence of a Δ1(ω1)-definable Bernstein subset of 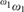${}_{}^{{\omega _1}}\omega _1^{}$. We also show that, if there are infinitely many Woodin cardinals and a measurable cardinal above them, then there is no Σ1(ω1)-definable uniformization of the club filter on ω1. Moreover, we prove a perfect set theorem for Σ1(ω1)-definable subsets of 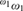${}_{}^{{\omega _1}}\omega _1^{}$, assuming that there is a measurable cardinal and the nonstationary ideal on ω1 is saturated. The proofs of these results use iterated generic ultrapowers and Woodin’s ℙmax-forcing. Finally, we also prove variants of some of these results for Σ1(κ)-definable subsets of κκ, in the case where κ itself has certain large cardinal properties.

Keywords

03E4503E4703E55Σ1-definabilitylightface formulaslarge cardinalswell-ordersclub filternonstationary idealBernstein setsiterated ultrapowersiterated generic ultrapowers
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 3 , September 2017 , pp. 1106 - 1131
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Caicedo, A. E. and Veličković, B., The bounded proper forcing axiom and well orderings of the reals . Mathematical Research Letters, vol. 13 (2006), no. 2–3, pp. 393–408.Google Scholar
Claverie, B. and Schindler, R., Woodin’s axiom (*), bounded forcing axioms, and precipitous ideals on ω 1, this Journal, vol. 77 (2012), no. 2, pp. 475–498.Google Scholar
Farah, I. and Larson, P. B., Absoluteness for universally Baire sets and the uncountable. I , Set Theory: Recent Trends and Applications (Andretta, A., editor), Quaderni di Matematica, vol. 17, Department of Mathematics, Seconda Universitá di Napoli, Caserta, 2006, pp. 47–92.Google Scholar
Friedman, S.-D. and Wu, L., Large cardinals and Δ1 -definablity of the nonstationary ideal, preprint.Google Scholar
Friedman, S.-D., Wu, L., and Zdomskyy, L., Δ1 -definability of the non-stationary ideal at successor cardinals . Fundamenta Mathematicae, vol. 229 (2015), no. 3, pp. 231–254.Google Scholar
Gitman, V., Ramsey-like cardinals, this Journal, vol. 76 (2011), no. 2, pp. 519–540.Google Scholar
Gitman, V. and Welch, P. D., Ramsey-like cardinals II, this Journal, vol. 76 (2011), no. 2, pp. 541–560.Google Scholar
Goldstern, M. and Shelah, S., The bounded proper forcing axiom, this Journal, vol. 60 (1995), no. 1, pp. 58–73.Google Scholar
Holy, P. and Lücke, P., Locally Σ1 -definable well-orders of H(κ +). Fundamenta Mathematicae, vol. 226 (2014), no. 3, pp. 221–236.Google Scholar
Holy, P. and Lücke, P., Simplest possible locally definable well-orders . Fundamenta Mathematicae, vol. 236 (2017), no. 2, pp. 101–139.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jech, T., Magidor, M., Mitchell, W. J., and Prikry, K., Precipitous ideals, this Journal, vol. 45 (1980), no. 1, pp. 1–8.Google Scholar
Jensen, R. and Steel, J. R., K without the measurable, this Journal, vol. 78 (2013), no. 3, pp. 708–734.Google Scholar
Kanamori, A., The Higher Infinite, second ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Larson, P. B., The Stationary Tower, University Lecture Series, vol. 32, American Mathematical Society, Providence, RI, 2004. Notes on a course by Hugh Woodin, W..Google Scholar
Larson, P. B., Forcing over models of determinacy , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 2121–2177.Google Scholar
Larson, P. B., A brief history of determinacy , The Handbook of the History of Logic, vol. 6 (Gabbay, D. M., Kanamori, A., and Woods, J., editors), Elsevier, Amsterdam, 2012, pp. 457–507.Google Scholar
Lücke, P., ${\rm{\Sigma }}_1^1$ -definability at uncountable regular cardinals, this Journal, vol. 77 (2012), no. 3, pp. 1011–1046.Google Scholar
Lücke, P., Motto Ros, L., and Schlicht, P., The Hurewicz dichotomy for generalized Baire spaces . Israel Journal of Mathematics, vol. 216 (2016), no. 2, pp. 973–1022.Google Scholar
Magidor, M., Precipitous ideals and ${\bf{\Sigma }}_4^1$ sets . Israel Journal of Mathematics, vol. 35 (1980), no. 1–2, pp. 109–134.Google Scholar
Mekler, A. and Väänänen, J., Trees and ${\rm{\Pi }}_1^1$ -subsets of ${}_{}^{{\omega _1}}\omega _1^{}$ , this Journal, vol. 58 (1993), no. 3, pp. 1052–1070.Google Scholar
Mitchell, W. J. and Steel, J. R., Fine Structure and Iteration Trees, Lecture Notes in Logic, vol. 3, Springer-Verlag, Berlin, 1994.Google Scholar
Moschovakis, Y. N., Descriptive Set Theory, second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.Google Scholar
Neeman, I., Optimal proofs of determinacy . Bulletin of Symbolic Logic, vol. 1 (1995), no. 3, pp. 327–339.Google Scholar
Schimmerling, E., A core model toolbox and guide , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 1685–1751.Google Scholar
Schindler, R., Semi-proper forcing, remarkable cardinals, and bounded Martin’s maximum. Mathematical Logic Quarterly, vol. 50 (2004), no. 6, pp. 527–532.Google Scholar
Schlicht, P., Thin equivalence relations and inner models . Annals of Pure and Applied Logic, vol. 165 (2014), no. 10, pp. 1577–1625.Google Scholar
Schlicht, P., Perfect subsets of generalized Baire spaces and long games, submitted.Google Scholar
Sharpe, I. and Welch, P. D., Greatly Erdős cardinals with some generalizations to the Chang and Ramsey properties . Annals of Pure and Applied Logic, vol. 162 (2011), no. 11, pp. 863–902.Google Scholar
Steel, J. R., Inner models with many Woodin cardinals . Annals of Pure and Applied Logic, vol. 65 (1993), no. 2, pp. 185–209.Google Scholar
Steel, J. R., An outline of inner model theory , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 1595–1684.Google Scholar
Steel, J. R., Introduction to iterated ultrapowers. Lecture notes.Google Scholar
Steel, J. R. and Woodin, W. H., HOD as a core model , Ordinal Definability and Recursion Theory. The Cabal Seminar, Volume III (Kechris, A. S., Lowe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 43, Association for Symbolic Logic, La Jolla, CA; Cambridge University Press, Cambridge, 2016, pp. 257–348.Google Scholar
Veličković, B. and Woodin, W. H., Complexity of reals in inner models of set theory . Annals of Pure and Applied Logic, vol. 92 (1998), no. 3, pp. 283–295.Google Scholar
Woodin, W. H., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, de Gruyter Series in Logic and its Applications, vol. 1, Walter de Gruyter & Co., Berlin, 1999.Google Scholar
Zeman, M., Inner Models and Large Cardinals, de Gruyter Series in Logic and its Applications, vol.5, Walter de Gruyter & Co., Berlin, 2002.Google Scholar