Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T17:45:34.968Z Has data issue: false hasContentIssue false
  • English
  • Français

AN AXIOMATIC APPROACH TO FREE AMALGAMATION

Published online by Cambridge University Press:  19 June 2017

GABRIEL CONANT
GABRIEL CONANT*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN 46656, USAE-mail: gconant@nd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We use axioms of abstract ternary relations to define the notion of a free amalgamation theory. These form a subclass of first-order theories, without the strict order property, encompassing many prominent examples of countable structures in relational languages, in which the class of algebraically closed substructures is closed under free amalgamation. We show that any free amalgamation theory has elimination of hyperimaginaries and weak elimination of imaginaries. With this result, we use several families of well-known homogeneous structures to give new examples of rosy theories. We then prove that, for free amalgamation theories, simplicity coincides with NTP2 and, assuming modularity, with NSOP3 as well. We also show that any simple free amalgamation theory is 1-based. Finally, we prove a combinatorial characterization of simplicity for Fraïssé limits with free amalgamation, which provides new context for the fact that the generic Kn-free graphs are SOP3, while the higher arity generic 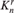$K_n^r$-free r-hypergraphs are simple.

Keywords

Primary 03C45Secondary 03C15free amalgamationhomogeneous structuressimplicityrosinessTP2SOPn
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 648 - 671
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., Explanation of independence, Ph.D. thesis, Albert-Ludwigs-Universität Freiburg, 2005.Google Scholar
Adler, H., A geometric introduction to forking and thorn-forking . Journal of Mathematical Logic, vol. 9 (2009), no. 1, pp. 1–20.Google Scholar
Casanovas, E., Simple Theories and Hyperimaginaries, Lecture Notes in Logic, vol. 39, Association for Symbolic Logic, Chicago, IL, 2011.Google Scholar
Casanovas, E. and Wagner, F. O., The free roots of the complete graph . Proceedings of the American Mathematical Society, vol. 132 (2004), no. 5, pp. 1543–1548.CrossRefGoogle Scholar
Cherlin, G., Shelah, S., and Shi, N., Universal graphs with forbidden subgraphs and algebraic closure . Advances in Applied Mathematics, vol. 22 (1999), no. 4, pp. 454–491.CrossRefGoogle Scholar
Conant, G., Neostability in countable homogeneous metric spaces, 2015, arXiv:1504.02427 [math.LO].Google Scholar
Conant, G. and Terry, C., Model theoretic properties of the Urysohn sphere . Annals of Pure and Applied Logic, vol. 167 (2016), no. 1, pp. 49–72.Google Scholar
Ealy, C. and Goldbring, I., Thorn-Forking in continuous logic, this Journal, vol. 77 (2012), no. 1, pp. 63–93.Google Scholar
Ealy, C. and Onshuus, A., Characterizing rosy theories, this Journal, vol. 72 (2007), no. 3, pp. 919–940.Google Scholar
Evans, D. M., ${\aleph _0}$ -categorical structures with a predimension . Annals of Pure and Applied Logic, vol. 116 (2002), no. 1–3, pp. 157–186.Google Scholar
Evans, D. M., Ghadernezhad, Z., and Tent, K., Simplicity of the automorphism groups of some Hrushovski constructions . Annals of Pure and Applied Logic, vol. 167 (2016), no. 1, pp. 22–48.Google Scholar
Evans, D. M. and Wong, M. W. H., Some remarks on generic structures, this Journal, vol. 74 (2009), no. 4, pp. 1143–1154.Google Scholar
Hart, B., Kim, B., and Pillay, A., Coordinatisation and canonical bases in simple theories, this Journal, vol. 65 (2000), no. 1, pp. 293–309.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.Google Scholar
Hrushovski, E., A new strongly minimal set . Annals of Pure and Applied Logic, vol. 62 (1993), no. 2, pp. 147–166, Stability in model theory, III (Trento, 1991).CrossRefGoogle Scholar
Hrushovski, E., Pseudo-finite fields and related structures , Model Theory and Applications, Quaderni di Matematica, vol. 11, Aracne, Rome, 2002, pp. 151–212.Google Scholar
Kim, B., Simplicity, and stability in there, this Journal, vol. 66 (2001), no. 2, pp. 822–836.Google Scholar
Kim, B., Simplicity Theory, Oxford Logic Guides, vol. 53, Oxford University Press, Oxford, 2014.Google Scholar
Kim, B. and Kim, H-J., Notions around tree property 1. Annals of Pure and Applied Logic, vol. 162 (2011), no. 9, pp. 698–709.Google Scholar
Komjáth, P., Some remarks on universal graphs . Discrete Mathematics, vol. 199 (1999), no. 1–3, pp. 259–265.Google Scholar
Koponen, V., Binary primitive homogeneous one-based structures, 2015, arXiv:1507.07360 [math.LO].Google Scholar
Macpherson, D. and Tent, K., Simplicity of some automorphism groups . Journal of Algebra, vol. 342 (2011), pp. 40–52.CrossRefGoogle Scholar
Onshuus, A., Properties and consequences of thorn-independence, this Journal, vol. 71 (2006), no. 1, pp. 1–21.Google Scholar
Palacín, D., Generalized amalgamation and homogeneity, 2016, arXiv:1603.09694 [math.LO].Google Scholar
Patel, R., A family of countably universal graphs without SOP4, unpublished, 2006.Google Scholar
Shelah, S., Toward classifying unstable theories. Annals of Pure and Applied Logic, vol. 80 (1996), no. 3, pp. 229–255.Google Scholar
Shelah, S. and Usvyatsov, A., Banach spaces and groups—order properties and universal models. Israel Journal of Mathematics, vol. 152 (2006), pp. 245–270.Google Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Lecture Notes in Logic, vol. 40, Association for Symbolic Logic, La Jolla, CA, 2012.Google Scholar
Tent, K. and Ziegler, M., On the isometry group of the Urysohn space . Journal of the London Mathematical Society(2), vol. 87 (2013), no. 1, pp. 289–303.Google Scholar
Wong, M. W. H., ${\aleph _0}$ -categorical Hrushovski constructions, strong order properties, oak and independence, Ph.D. thesis, University of East Anglia, 2007.Google Scholar