Article contents
An incomplete decidable modal logic
Published online by Cambridge University Press: 12 March 2014
Extract
The most common way of proving decidability in propositional modal logic is to shew that the system in question has the finite model property. This is not however the only way. Gabbay in [4] proves the decidability of many modal systems using Rabin's result in [8] on the decidability of the second-order theory of successor functions. In particular [4, pp. 258-265] he is able to prove the decidability of a system which lacks the finite model property. Gabbay's system is however complete, in the sense of being characterized by a class of frames, and the question arises whether there is a decidable modal logic which is not complete. Since no incomplete modal logic has the finite model property [9, p. 33], any proof of decidability must employ some such method as Gabbay's. In this paper I use the Gabbay/Rabin technique to prove the decidability of a finitely axiomatized normal modal propositional logic which is not characterized by any class of frames. I am grateful to the referee for suggesting improvements in substance and presentation.
The terminology I am using is standard in modal logic. By a frame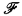 is understood a pair 〈W, R〉 in which W is a class (of “possible worlds”) and R ⊆ W2. To avoid confusion in what follows, a frame will henceforth be referred to as a Kripke frame. By contrast, a general frame
is understood a pair 〈W, R〉 in which W is a class (of “possible worlds”) and R ⊆ W2. To avoid confusion in what follows, a frame will henceforth be referred to as a Kripke frame. By contrast, a general frame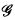 is a pair 〈
is a pair 〈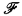 , Π〉 in which
, Π〉 in which 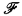 is a Kripke frame and Π is a collection of subsets of W closed under the Boolean operations and satisfying the condition that if A is in Π then so is R−1 “A. A model on a frame (of either kind) is obtained by adding a function V which assigns sets of worlds to propositional variables. In the case of a general frame we require that V(p) ∈ Π.
is a Kripke frame and Π is a collection of subsets of W closed under the Boolean operations and satisfying the condition that if A is in Π then so is R−1 “A. A model on a frame (of either kind) is obtained by adding a function V which assigns sets of worlds to propositional variables. In the case of a general frame we require that V(p) ∈ Π.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 7
- Cited by

