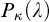Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matet, Pierre
2022.
The secret life of μ-clubs.
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 9,
p.
103162.
Matet, Pierre
2024.
Meeting, covering and Shelah's Revised GCH.
Topology and its Applications,
Vol. 356,
Issue. ,
p.
109044.
Matet, Pierre
2024.
Good points for scales (and more).
Mathematical Logic Quarterly,
Vol. 70,
Issue. 3,
p.
333.
Matet, Pierre
2025.
μ-clubs of P(λ): Paradise in heaven.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 1,
p.
103497.