Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-30T21:43:57.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphism groups of models of Peano arithmetic

Published online by Cambridge University Press:  12 March 2014

James H. Schmerl
James H. Schmerl*
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Ct 06269., USA, E-mail: schmerl@math.uconn.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Which groups are isomorphic to automorphism groups of models of Peano Arithmetic? It will be shown here that any group that has half a chance of being isomorphic to the automorphism group of some model of Peano Arithmetic actually is.

For any structure 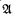, let Aut(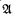) be its automorphism group. There are groups which are not isomorphic to any model 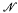= (N, +, ·, 0, 1, ≤) of PA. For example, it is clear that Aut(N), being a subgroup of Aut((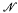, <)), must be torsion-free. However, as will be proved in this paper, if (A, <) is a linearly ordered set and G is a subgroup of Aut((A, <)), then there are models 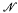of PA such that Aut(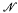) ≅ G.

If 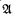is a structure, then its automorphism group can be considered as a topological group by letting the stabilizers of finite subsets of A be the basic open subgroups. If 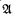′ is an expansion of 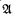, then Aut(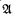′) is a closed subgroup of Aut(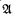). Conversely, for any closed subgroup G ≤ Aut(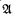) there is an expansion 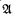′ of 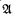such that Aut(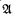′) = G. Thus, if 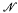is a model of PA, then Aut(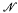) is not only a subgroup of Aut((N, <)), but it is even a closed subgroup of Aut((N, ′)).

There is a characterization, due to Cohn [2] and to Conrad [3], of those groups G which are isomorphic to closed subgroups of automorphism groups of linearly ordered sets.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 4 , December 2002 , pp. 1249 - 1264
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Abramson, F. G. and Harrington, L. A., Models without indiscernibles, this Journal, vol. 43 (1978), pp. 572–600.Google Scholar
[2]Cohn, P. M., Groups of order automorphisms of ordered sets, Mathematika, vol. 4 (1957), pp. 41–50.CrossRefGoogle Scholar
[3]Conrad, P., Right-ordered groups, Michigan Mathematical Journal, vol. 6 (1959), pp. 267–275.CrossRefGoogle Scholar
[4]Dugas, M. and Göbel, R., All infinite groups are Galois groups over any field, Transactions of the American Mathematical Society, vol. 304 (1987), pp. 355–384.CrossRefGoogle Scholar
[5]Ehrenfeucht, A., Discernible elements in models of Peano arithmetic, this Journal, vol. 38 (1973), pp. 291–292.Google Scholar
[6]Gaifman, H., On models and types of Peano's arithmetic, Annals of Mathematical Logic, vol. 9 (1976), pp. 223–306.CrossRefGoogle Scholar
[7]Glass, A., Ordered permutation groups, London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, 1981.Google Scholar
[8]Kaye, R., Models of Peano arithmetic, Oxford Logic Guides, Oxford University Press, Oxford, 1991.CrossRefGoogle Scholar
[9]Kaye, R., Kossak, R., and Kotlarski, H., Automorphisms of recursively saturated models of arithmetic, Annals of Pure and Applied Logic, vol. 55 (1991), pp. 67–99.CrossRefGoogle Scholar
[10]Kirby, L. A. S. and Paris, J. B., Initial segments of models of Peano's axioms, Set theory and hierarchy theory V, Bierutowice, Poland, 1976 (Lachlan, A.et al., editor), Lecture Notes in Mathematics, no. 619, 1977, pp. 221–226.Google Scholar
[11]Kopytov, V. M. and Medvedev, N. Y., Right-orderable groups, Consultants Bureau, New York, 1996.Google Scholar
[12]Kossak, R., Satisfaction classes and automorphisms of models of PA, Logic colloquium '96, Proceedings of the colloquium held in San Sebastián, Spain, July 9–15, 1996, Springer-Verlag, Berlin, 1998, pp. 159–170.Google Scholar
[13]Kossak, R. and Bamber, N., On two questions concerning the automorphism groups of countable recursively saturated models of PA, Archive for Mathematical Logic, vol. 36 (1996), pp. 73–79.CrossRefGoogle Scholar
[14]Kossak, R. and Schmerl, J. H., Minimal satisfaction classes with an application to rigid models of Peano arithmetic, Notre Dame Journal of Formal Logic, vol. 32 (1991), pp. 392–398.CrossRefGoogle Scholar
[15]Kossak, R. and Schmerl, J. H., Arithmetically saturated models of arithmetic, Notre Dame Journal of Formal Logic, vol. 36 (1995), pp. 531–546.CrossRefGoogle Scholar
[16]Kossak, R. and Schmerl, J. H., The automorphism group of an arithmetically saturated model of Peano arithmetic, Journal of the London Mathematical Society, vol. 52 (1995), no. 2, pp. 235–244.CrossRefGoogle Scholar
[17]Nešetřil, J. and Rödl, V., Partitions of finite relational and set systems, Journal of Combinatorial Theory A, vol. 22 (1977), pp. 289–312.CrossRefGoogle Scholar
[18]Robinson, J., Decidability and decision problems in arithmetic, this Journal, vol. 14 (1949), pp. 98–114.Google Scholar
[19]Schmerl, J. H., Recursively saturated, rather classless models of Peano arithmetic, Logic year 1979–80, University of Connecticut (Lerman, M.et al., editor), Lecture Notes in Mathematics, no. 859, Springer-Verlag, Berlin, 1981, pp. 268–82.CrossRefGoogle Scholar
[20]Smoryński, C. A. and Stavi, J., Cofinal extension preserves recursive saturation, Model theory of algebra and arithmetic, Proceedings, Karpacz, Poland, 1978 (Pacholski, L.et al., editor), Lecture Notes in Mathematics, no. 834, Springer-Verlag, Berlin, 1980, pp. 338–345.Google Scholar