Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T18:08:21.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Bad models in nice neighborhoods

Published online by Cambridge University Press:  12 March 2014

Terry Millar
Terry Millar*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Extract

This paper contains an example of a decidable theory which has

1) only a countable number of countable models (up to isomorphism);

2) a decidable saturated model; and

3) a countable homogeneous model that is not decidable.

By the results in [1] and [2], this can happen if and only if the set of types realized by the homogeneous model (the type spectrum of the model) is not .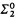

If Γ and Σ are types of a theory T, define Γ ◁ Σ to mean that any model of T realizing Γ must realize Σ. In [3] a decidable theory is constructed that has only countably many countable models, only recursive types, but whose countable saturated model is not decidable. This is easy to do if the restriction on the number of countable models is lifted; the difficulty arises because the set of types must be recursively complex, and yet sufficiently related to control the number of countable models. In [3] the desired theory T is such that

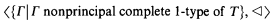
is a linear order with order type ω*. Also, the set of complete types of T is not 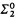. The last feature ensures that the countable saturated model is not decidable; the first feature allows the number of countable models to be controlled.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 4 , December 1986 , pp. 1043 - 1055
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Millar, T., Foundations of recursive model theory, Annals of Mathematical Logic, vol. 13 (1978), pp. 45–72.CrossRefGoogle Scholar
[2]Millar, T., Type structure of complexity and decidability, Transactions of the American Mathematical Society, vol. 271 (1981), pp. 73–81.CrossRefGoogle Scholar
[3]Millar, T., Decidability and the number of countable models, Annals of Pure and Applied Logic, vol. 27 (1984), pp. 137–153.CrossRefGoogle Scholar
[4]Millar, T., Counterexamples via model completions, Logic year 1979–80, Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 215–229.CrossRefGoogle Scholar