Article contents
Beth definability in infinitary languages
Published online by Cambridge University Press: 12 March 2014
Extract
Some negative results will be proved concerning the following for certain infinitary languages ℒ1 and ℒ2.
Definition. Beth(ℒ1, ℒ2) iff, for every sentence ϕ(R) of ℒ1, and n-place relation symbols R and S such that S does not occur in ϕ(R), if
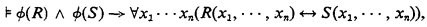
then there is an ℒ2 formula θ(x1, …, xn) such that
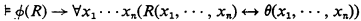
and θ is built up using only those constant and relation symbols of ϕ other than R.
That is, Beth(ℒ1, ℒ2) iff for every implicit ℒ1 definition ϕ(R) of relations, there is a corresponding explicit ℒ2 definition θ. Beth(ℒωω, ℒωω) was proved by Beth.
Malitz proved that not Beth(ℒω1 ω1, ℒ∞∞) (hence not Beth (ℒ∞∞, ℒ∞∞)), but Beth (ℒ∞ω, ℒ∞∞). In §1, it is shown that Beth(ℒ∞ω, ℒ∞ω) is false. In §2, we strengthen this by showing that, for every cardinal κ, not Beth(ℒ∞ω, ℒ∞κ). In fact, not Beth (ℒκ+ω, ℒ∞κ) follows from property A(κ) defined in §2, and A(κ) is known for regular κ > ω (unpublished result of Morley).
More information on infinitary Beth and Craig theorems is given in [2] and [3]. We assume that the reader is acquainted with the languages ℒκλ which allow conjunctions over ≺κ formulas and quantifiers over ≺λ variables. Thus, we assume that the reader is acquainted with the back and forth argument for showing that two structures are ≡∞κ (ℒ∞κ-elementarily equivalent). Our notation is fairly standard.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 7
- Cited by

