Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T12:15:30.484Z Has data issue: false hasContentIssue false
  • English
  • Français

BINARY PRIMITIVE HOMOGENEOUS SIMPLE STRUCTURES

Published online by Cambridge University Press:  21 March 2017

VERA KOPONEN
VERA KOPONEN*
Affiliation:
DEPARTMENT OF MATHEMATICS UPPSALA UNIVERSITY BOX 480, 75106 UPPSALA, SWEDENE-mail: vera.koponen@math.uu.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 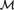${\cal M}$ is countable, binary, primitive, homogeneous, and simple. We prove that the SU-rank of the complete theory of 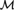${\cal M}$ is 1 and hence 1-based. It follows that 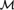${\cal M}$ is a random structure. The conclusion that 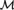${\cal M}$ is a random structure does not hold if the binarity condition is removed, as witnessed by the generic tetrahedron-free 3-hypergraph. However, to show that the generic tetrahedron-free 3-hypergraph is 1-based requires some work (it is known that it has the other properties) since this notion is defined in terms of imaginary elements. This is partly why we also characterize equivalence relations which are definable without parameters in the context of ω-categorical structures with degenerate algebraic closure. Another reason is that such characterizations may be useful in future research about simple (nonbinary) homogeneous structures.

Keywords

03C1003C5003C45model theoryhomogeneous structuresimple theory1-based theoryrandom structure
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 183 - 207
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., A geometric introduction to forking and thorn-forking . Journal of Mathematical Logic, vol. 9 (2009), pp. 1–20.CrossRefGoogle Scholar
Ahlman, O. and Koponen, V., On sets with rank one in simple homogeneous structures . Fundamenta Mathematicae, vol. 228 (2015), pp. 223–250.CrossRefGoogle Scholar
Aranda López, A., Omega-categorical Simple Theories, Ph.D. thesis, The University of Leeds, 2014.Google Scholar
Cherlin, G. L., The Classification of Countable Homogeneous Directed Graphs and Countable Homogeneous n-tournaments, Memoirs of the American Mathematical Society 621, American Mathematical Society, Providence, 1998.CrossRefGoogle Scholar
Conant, G., An axiomatic approach to free amalgamation, available at http://arxiv.org/abs/1505.00762.Google Scholar
De Piro, T. and Kim, B., The geometry of 1-based minimal types . Transactions of The American Mathematical Society, vol. 355 (2003), pp. 4241–4263.CrossRefGoogle Scholar
Djordjević, M., The finite submodel property and ω-categorical expansions of pregeometries . Annals of Pure and Applied Logic, vol. 139 (2006), pp. 201–229.Google Scholar
Djordjević, M., Finite satisfiability and ${\aleph _0}$ -categorical structures with trivial dependence, this Journal, vol. 71 (2006), pp. 810–829.Google Scholar
Goode, J. B., Some trivial considerations, this Journal, vol. 56 (1991), pp. 624–631.Google Scholar
Hart, B., Kim, B., and Pillay, A., Coordinatisation and canonical bases in simple theories, this Journal, vol. 65 (2000), pp. 293–309.Google Scholar
Hodges, W., Model Theory, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Koponen, V., Binary simple homogeneous structures are supersimple with finite rank . Proceedings of the American Mathematical Society, vol. 144 (2016), pp. 1745–1759.CrossRefGoogle Scholar
Koponen, V., Homogeneous 1-based structures and interpretability in random structures . Mathematical Logic Quarterly, available at http://arxiv.org/abs/1403.3757.Google Scholar
Lachlan, A. H., Stable finitely homogeneous structures: A survey, Algebraic Model Theory (Hart, B. T., Lachlan, A. H., and Valeriote, M. A., editors), Kluwer Academic Publishers, Dordrecht, 1997, pp. 145–159.CrossRefGoogle Scholar
Macpherson, D., Interpreting groups in ω-categorical structures, this Journal, vol. 56 (1991), pp. 1317–1324.Google Scholar
Macpherson, D., A survey of homogeneous structures . Discrete Mathematics, vol. 311 (2011), pp. 1599–1634.CrossRefGoogle Scholar
Palacín, D., Generalized amalgamation and homogeneity, available at http://arxiv.org/abs/1603.09694v2.Google Scholar
Wagner, F. O., Simple Theories, Kluwer Academic Publishers, 2000.Google Scholar