Article contents
Blunt and topless end extensions of models of set theory
Published online by Cambridge University Press: 12 March 2014
Abstract
Let 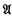 be a well-founded model of ZFC whose class of ordinals has uncountable cofinality, such that
be a well-founded model of ZFC whose class of ordinals has uncountable cofinality, such that 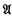 has a Σn end extension for each n ∈ ω. It is shown in Theorem 1.1 that there is such a model which has no elementary end extension. In the process some interesting facts about topless end extensions (those with no least new ordinal) are uncovered, for example Theorem 2.1: If
has a Σn end extension for each n ∈ ω. It is shown in Theorem 1.1 that there is such a model which has no elementary end extension. In the process some interesting facts about topless end extensions (those with no least new ordinal) are uncovered, for example Theorem 2.1: If 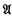 is a well-founded model of ZFC, such that
is a well-founded model of ZFC, such that 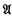 has uncountable cofinality and
has uncountable cofinality and 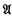 has a topless Σ3 end extension, then
has a topless Σ3 end extension, then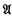 has a topless elementary end extension and also a well-founded elementary end extension, and contains ordinals which are (in
has a topless elementary end extension and also a well-founded elementary end extension, and contains ordinals which are (in 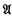 ) highly hyperinaccessible. In §3 related results are proved for κ-like models (κ any regular cardinal) which need not be well founded. As an application a soft proof is given of a theorem of Schmerl on the model-theoretic relation κ → λ. (The author has been informed that Silver had earlier, independently, found a similar unpublished proof of that theorem.) Also, a simpler proof is given of (a generalization of) a characterization by Keisler and Silver of the class of well-founded models which have a Σn end extension for each n ∈ ω. The case κ = ω1 is investigated more deeply in §4, where the problem solved by Theorem 1.1 is considered for non-well-founded models. In Theorems 4.1 and 4.4, ω1-like models of ZFC are constructed which have a Σn end extension for all n ∈ ω but have no elementary end extension. ω1-like models of ZFC which have no Σ3 end extension are produced in Theorem 4.2. The proof uses a notion of satisfaction class, which is also applied in the proof of Theorem 4.6: No model of ZFC has a definable end extension which satisfies ZFC. Finally, Theorem 5.1 generalizes results of Keisler and Morley, and Hutchinson, by asserting that every model of ZFC of countable cofinality has a topless elementary end extension. This contrasts with the rest of the paper, which shows that for well-founded models of uncountable cofinality and for κ-like models with κ regular, topless end extensions are much rarer than blunt end extensions.
) highly hyperinaccessible. In §3 related results are proved for κ-like models (κ any regular cardinal) which need not be well founded. As an application a soft proof is given of a theorem of Schmerl on the model-theoretic relation κ → λ. (The author has been informed that Silver had earlier, independently, found a similar unpublished proof of that theorem.) Also, a simpler proof is given of (a generalization of) a characterization by Keisler and Silver of the class of well-founded models which have a Σn end extension for each n ∈ ω. The case κ = ω1 is investigated more deeply in §4, where the problem solved by Theorem 1.1 is considered for non-well-founded models. In Theorems 4.1 and 4.4, ω1-like models of ZFC are constructed which have a Σn end extension for all n ∈ ω but have no elementary end extension. ω1-like models of ZFC which have no Σ3 end extension are produced in Theorem 4.2. The proof uses a notion of satisfaction class, which is also applied in the proof of Theorem 4.6: No model of ZFC has a definable end extension which satisfies ZFC. Finally, Theorem 5.1 generalizes results of Keisler and Morley, and Hutchinson, by asserting that every model of ZFC of countable cofinality has a topless elementary end extension. This contrasts with the rest of the paper, which shows that for well-founded models of uncountable cofinality and for κ-like models with κ regular, topless end extensions are much rarer than blunt end extensions.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 6
- Cited by

