Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T17:44:38.008Z Has data issue: false hasContentIssue false
  • English
  • Français

CALIBRATING DETERMINACY STRENGTH IN LEVELS OF THE BOREL HIERARCHY

Published online by Cambridge University Press:  19 June 2017

SHERWOOD HACHTMAN
SHERWOOD HACHTMAN*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA, LOS ANGELES LOS ANGELES, CA90024, USA E-mail: hachtma1@uic.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze the set-theoretic strength of determinacy for levels of the Borel hierarchy of the form 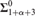$\Sigma _{1 + \alpha + 3}^0 $, for α < ω1. Well-known results of H. Friedman and D.A. Martin have shown this determinacy to require α + 1 iterations of the Power Set Axiom, but we ask what additional ambient set theory is strictly necessary. To this end, we isolate a family of weak reflection principles, Π1-RAPα, whose consistency strength corresponds exactly to the logical strength of 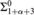${\rm{\Sigma }}_{1 + \alpha + 3}^0 $ determinacy, for 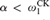$\alpha < \omega _1^{CK} $. This yields a characterization of the levels of L by or at which winning strategies in these games must be constructed. When α = 0, we have the following concise result: The least θ so that all winning strategies in 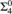${\rm{\Sigma }}_4^0 $ games belong to Lθ+1 is the least so that 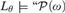$L_\theta \models {\rm{``}}{\cal P}\left( \omega \right)$ exists, and all wellfounded trees are ranked”.

Keywords

03F3503E60Borel determinacyadmissible setsreflectioninductive definability
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 510 - 548
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barwise, J., Admissible Sets and Structures, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1975.Google Scholar
Blass, A., Complexity of winning strategies . Discrete Mathematics, vol. 3 (1972), pp. 295–300.Google Scholar
Davis, M., Infinite games of perfect information , Advances in Game Theory (Dresher, M., Shapley, L. S., and William Tucker, A., editors), Princeton University Press, Princeton, NJ, 1964, pp. 85–101.Google Scholar
Friedman, H. M., Higher set theory and mathematical practice . Annals of Mathematical Logic, vol. 2 (1970/1971), no. 3, pp. 325–357.Google Scholar
Gale, D. and Stewart, F. M., Infinite games with perfect information , Contributions to the Theory of Games, vol. 2, Annals of Mathematics Studies, no. 28, Princeton University Press, Princeton, NJ, 1953, pp. 245–266.Google Scholar
Hurkens, A. J. C., Borel determinacy without the axiom of choice, Ph.D. thesis, Katholieke Universiteit Nijmegen, Nijmegen, The Netherlands, 1993.Google Scholar
Jensen, R. B., The fine structure of the constructible hierarchy . Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308; erratum, ibid. 4(1972), 443, with a section by Jack Silver.CrossRefGoogle Scholar
Kechris, A. S., On spector classes , Ordinal Definability and Recursion Theory: The Cabal Seminar, vol. III (Kechris, A., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 43, Cambridge University Press, Cambridge, 2016, pp. 390–423.Google Scholar
Martin, D. A., A purely inductive proof of Borel determinacy , Recursion Theory (Ithaca, NY, 1982) (Nerode, A. and Shore, R. A., editors), Proceedings of the Symposium on Pure Mathematics, vol. 42, American Mathematical Society, Providence, RI, 1985, pp. 303–308.Google Scholar
Martin, D. A., ${\rm{\Pi }}_2^1 $ monotone inductive definitions , Ordinal Definability and Recursion Theory: The Cabal Seminar, vol. III (Kechris, A., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 43, Cambridge University Press, Cambridge, 2016, pp. 476–492.Google Scholar
Martin, D. A., Determinacy, unpublished manuscript, Available at http://www.math.ucla.edu/~ dam/booketc/thebook.pdf (accessed 23 February, 2017).Google Scholar
Montalbán, A. and Shore, R. A., The limits of determinacy in second-order arithmetic . Proceedings of the London Mathematical Society (3), vol. 104 (2012), no. 2, pp. 223–252.CrossRefGoogle Scholar
Moschovakis, Y. N., Descriptive Set Theory, second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.Google Scholar
Schindler, R. and Zeman, M., Fine structure , Handbook of set theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 605–656.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge; Association for Symbolic Logic, Poughkeepsie, NY, 2009.Google Scholar
Steel, J. R., Determinateness and subsystems of analysis, Ph.D. thesis, ProQuest LLC, Ann Arbor, MI, University of California, Berkeley, 1977.Google Scholar
Tanaka, K., Weak axioms of determinacy and subsystems of analysis. II. ${\rm{\Sigma }}_2^0 $ games . Annals of Pure and Applied Logic, vol. 52 (1991), no. 1–2, pp. 181–193, International Symposium on Mathematical Logic and its Applications (Nagoya, 1988).Google Scholar
Welch, P. D., Weak systems of determinacy and arithmetical quasi-inductive definitions , this Journal, vol. 76 (2011), no. 2, pp. 418–436.Google Scholar
Welch, P. D., $G_{\delta \sigma } $ Games, Isaac Newton Institute Preprint Series, Cambridge University Press, Cambridge, UK, 2012, pp. 1–10.Google Scholar
Wolfe, P., The strict determinateness of certain infinite games . Pacific Journal of Mathematics, vol. 5 (1955), pp. 841–847.Google Scholar