Article contents
Choice principles, the bar rule and autonomously iterated comprehension schemes in analysis
Published online by Cambridge University Press: 12 March 2014
Extract
In [10] Friedman showed that (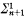 -AC) is a conservative extension of (
-AC) is a conservative extension of ( -CA)<ε0 for
-CA)<ε0 for 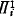 -sentences where i = min(n + 2, 4), i.e., i = 2, 3, 4 for n = 0, 1, 2 + m. Feferman [5], [7] and Tait [11], [12] reobtained this result for n = 0, 1 and even with (
-sentences where i = min(n + 2, 4), i.e., i = 2, 3, 4 for n = 0, 1, 2 + m. Feferman [5], [7] and Tait [11], [12] reobtained this result for n = 0, 1 and even with (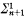 -DC) instead of (
-DC) instead of (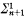 -AC). Feferman and Sieg established in [9] the conservativeness of (
-AC). Feferman and Sieg established in [9] the conservativeness of (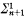 -DC) over (
-DC) over ( -CA)<ε0 for
-CA)<ε0 for 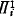 -sentences (i as above) for all n. In each paper, different methods of proof have been used. In particular, Feferman and Sieg showed how to apply familiar proof-theoretical techniques by passing through languages with Skolem functionals.
-sentences (i as above) for all n. In each paper, different methods of proof have been used. In particular, Feferman and Sieg showed how to apply familiar proof-theoretical techniques by passing through languages with Skolem functionals.
In this paper we study the same choice principles in the presence of the Bar Rule (BR), which permits one to infer the scheme of transfinite induction on a primitive recursive relation ≺ when it has been proved that ≺ is wellfounded. The main result (Theorem 1 below) characterizes (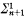 -DC) + (BR) as a conservative extension of a system of the autonomously iterated
-DC) + (BR) as a conservative extension of a system of the autonomously iterated  -comprehension axiom for
-comprehension axiom for 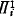 -sentences (i depending on n as above). For n = 0 this has been proved by Feferman in the form that (
-sentences (i depending on n as above). For n = 0 this has been proved by Feferman in the form that (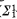 -DC) + (BR) is a conservative extension of (
-DC) + (BR) is a conservative extension of (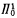 -CA)<Γ0; this was first done in [8] by use of the Gödel functional interpretation for the stronger system Zω + μ + (QF-AC) + (BR) and then more recently by the simpler methods of [9]. Jäger showed how the latter methods could also be used to obtain the general result of Theorem 1 below.
-CA)<Γ0; this was first done in [8] by use of the Gödel functional interpretation for the stronger system Zω + μ + (QF-AC) + (BR) and then more recently by the simpler methods of [9]. Jäger showed how the latter methods could also be used to obtain the general result of Theorem 1 below.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 7
- Cited by

