Article contents
Completeness theorem for biprobability models
Published online by Cambridge University Press: 12 March 2014
Extract
The aim of the paper is to prove the completeness theorem for biprobability models. This also solves Keisler's Problem 5.4 (see [4]).
Let 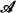 be a countable admissible set and ω ∈
be a countable admissible set and ω ∈ 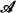 . The logic
. The logic 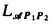 is similar to the standard probability logic
is similar to the standard probability logic 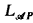 . The only difference is that two types of probability quantifiers
. The only difference is that two types of probability quantifiers 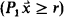 and
and 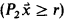 are allowed.
are allowed.
A biprobability model is a structure (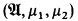 , μ1, μ2) where
, μ1, μ2) where 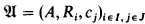 is a classical structure without operations and μ1, μ2 are two types of probability measures such that μ1 is absolutely continuous with respect to μ2, i.e. μ1 ≪ μ2.
is a classical structure without operations and μ1, μ2 are two types of probability measures such that μ1 is absolutely continuous with respect to μ2, i.e. μ1 ≪ μ2.
The quantifiers are interpreted in the natural way, i.e.
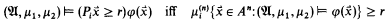
for i = 1, 2. (The measure 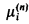 is the restriction of the completion of
is the restriction of the completion of 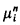 to the σ-algebra generated by the measurable rectangles and the diagonal sets
to the σ-algebra generated by the measurable rectangles and the diagonal sets 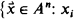
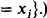
Axioms and rules of inference are those of 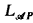 , as listed in [2] with the axiom B4 from [4], with the remark that both P1 and P2 can play the role of P, together with the following axioms:
, as listed in [2] with the axiom B4 from [4], with the remark that both P1 and P2 can play the role of P, together with the following axioms:
Axioms of continuity.
1)
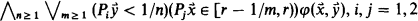 .
.2)
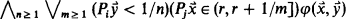 .
.
Axiom of absolute continuity:
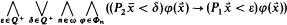
where 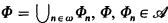 and Φn = {φ ∈ Φ: φ has n free variables}.
and Φn = {φ ∈ Φ: φ has n free variables}.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1986
References
REFERENCES
- 13
- Cited by

