Article contents
Computability and the algebra of fields: Some affine constructions
Published online by Cambridge University Press: 12 March 2014
Extract
A natural way of studying the computability of an algebraic structure or process is to apply some of the theory of the recursive functions to the algebra under consideration through the manufacture of appropriate coordinate systems from the natural numbers. An algebraic structure A = (A; σ1,…, σk) is computable if it possesses a recursive coordinate system in the following precise sense: associated to A there is a pair (α, Ω) consisting of a recursive set of natural numbers Ω and a surjection α: Ω → A so that (i) the relation defined on Ω by n ≡α m iff α(n) = α(m) in A is recursive, and (ii) each of the operations of A may be effectively followed in Ω, that is, for each (say) r-ary operation σ on A there is an r argument recursive function  on Ω which commutes the diagram
on Ω which commutes the diagram
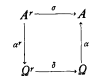
wherein αr is r-fold α × … × α.
This concept of a computable algebraic system is the independent technical idea of M.O.Rabin [18] and A.I.Mal'cev [14]. From these first papers one may learn of the strength and elegance of the general method of coordinatising; note-worthy for us is the fact that computability is a finiteness condition of algebra—an isomorphism invariant possessed of all finite algebraic systems—and that it serves to set upon an algebraic foundation the combinatorial idea that a system can be combinatorially presented and have effectively decidable term or word problem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1980
References
REFERENCES
- 7
- Cited by

