Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T09:07:59.949Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABILITY IN UNCOUNTABLE BINARY TREES

Published online by Cambridge University Press:  12 March 2019

REESE JOHNSTON
REESE JOHNSTON*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN-MADISON 480 LINCOLN DRIVE MADISON, WI 53706, USAE-mail: rwjohnston@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Computability, while usually performed within the context of ω, may be extended to larger ordinals by means of α-recursion. In this article, we concentrate on the particular case of ω1-recursion, and study the differences in the behavior of 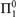${\rm{\Pi }}_1^0$-classes between this case and the standard one.

Of particular interest are the 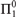${\rm{\Pi }}_1^0$-classes corresponding to computable trees of countable width. Classically, it is well-known that the analog to König’s Lemma—“every tree of countable width and uncountable height has an uncountable branch”—fails; we demonstrate that not only does it fail effectively, but also that the failure is as drastic as possible. This is proven by showing that the ω1-Turing degrees of even isolated paths in computable trees of countable width are cofinal in the 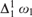${\rm{\Delta }}_1^1\,{\omega _1}$-Turing degrees.

Finally, we consider questions of nonisolated paths, and demonstrate that the degrees realizable as isolated paths and the degrees realizable as nonisolated ones are very distinct; in particular, we show that there exists a computable tree of countable width so that every branch can only be ω1-Turing equivalent to branches of trees with 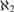${\aleph _2}$-many branches.

Keywords

Primary 03D60computabilityrecursion theoryadmissible recursion theoryset theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1049 - 1098
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, C. J., Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees. Transactions of the American Mathematical Society, vol. 298 (1986), no. 2, pp. 497–514.Google Scholar
Chong, C.-T., Techniques of Admissible Recursion Theory, Springer, Berlin, 1984.Google Scholar
Fokina, E., Friedman, S. D., Knight, J., and Miller, R., Classes of structures with universe a subset of ω1. Journal of Logic and Computation, vol. 23 (2013), no. 6, pp. 1249–1265.Google Scholar
Friedman, S. D., Negative solutions to Post’s problem, II. The Annals of Mathematics, Second Series, vol. 113 (1981), no. 1, pp. 25–43.Google Scholar
Gödel, K., The consistency of the axiom of choice and of the generalized continuum hypothesis. Proceedings of the National Academy of Sciences of the United States of America, vol. 24 (1938), no. 12, pp. 556–557.Google Scholar
Greenberg, N., The role of true finiteness in the admissible recursively enumerable degrees. The Bulletin of Symbolic Logic, vol. 11 (2005), no. 03, pp. 398–410.Google Scholar
Greenberg, N. and Knight, J., Computable structure theory using admissible recursion theory on ω1, Effective Mathematics of the Uncountable (Hamkins, J. D., Greenberg, N., Hirschfeldt, D., and Miller, R., editors), Cambridge University Press, Cambridge, 2013, pp. 50–80.Google Scholar
Greenberg, N. and Turetsky, D., unpublished notes, 2014.Google Scholar
Jensen, B. R., The fine structure of the constructible hierarchy, Annals of Mathematical Logic, vol. 4 (1972), no. 3, pp. 229–308.Google Scholar
Jockusch, C. G. Jr. and Soare, R. I., ${\rm{\Pi }}_1^0$ classes and degrees of theories. Transactions of the American Mathematics Society, vol. 173 (1972), pp. 33–56.Google Scholar
Koepke, P. and Seyfferth, B., Ordinal machines and admissible recursion theory. Annals of Pure and Applied Logic, vol. 160 (2009), pp. 310–318.Google Scholar
Kreisel, G., Some reasons for generalizing recursion theory, Logic Colloqium ’69 (Gandy, R. O. and Yates, C. M. E., editors), North Holland, Amsterdam, 1971, pp. 139–198.Google Scholar
Kreisel, G. and Sacks, G. E., Metarecursive sets, this Journal, vol. 30 (1965), no. 3, pp. 318–338.Google Scholar
Kripke, S., Transfinite recursion on admissible ordinals, this Journal, vol. 29 (1964), pp. 161–162.Google Scholar
Kunen, K., Set Theory: An Introduction to Independence Proofs, Elsevier, London, 2014.Google Scholar
Kurepa, G., Ensembles ordonnés et ramifiés. Publications mathématique University of Belgrade, vol. 4 (1935), pp. 1–138.Google Scholar
Montalbán, A., Priority arguments via true stages, this Journal, vol. 79 (2014), pp. 1001–1019.Google Scholar
Platek, R. A., Foundations of recursion theory, Ph.D. thesis, Stanford University, 1966.Google Scholar
Sacks, G. E., Higher Recursion Theory, Springer-Verlag, Berlin, 1990.Google Scholar
Shore, R., Reverse mathematics, countable and uncountable: A computational approach, Effective Mathematics of the Uncountable (Hamkins, J. D., Greenberg, N., Hirschfeldt, D., and Miller, R., editors), Cambridge University Press, Cambridge, 2013, pp. 150–163.Google Scholar
Simpson, S., Subsystems of Second Order Arithmetic, Springer, New York, 1999.Google Scholar