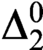Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Brecht, Matthew
Kihara, Takayuki
and
Selivanov, Victor
2022.
Revolutions and Revelations in Computability.
Vol. 13359,
Issue. ,
p.
88.
Bazhenov, Nikolay
Harrison-Trainor, Matthew
and
Melnikov, Alexander
2023.
Computable Stone spaces.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 9,
p.
103304.
Melnikov, Alexander G.
and
Ng, Keng Meng
2023.
Separating notions in effective topology.
International Journal of Algebra and Computation,
Vol. 33,
Issue. 08,
p.
1687.
Camrud, Caleb
Goldbring, Isaac
and
McNicholl, Timothy H.
2023.
On the complexity of the theory of a computably presented metric structure.
Archive for Mathematical Logic,
Vol. 62,
Issue. 7-8,
p.
1111.
Bazhenov, Nikolay
Kihara, Takayuki
Selivanova, Svetlana
Spreen, Dieter
Bazhenov, Nikolay
Kihara, Takayuki
and
Selivanova, Svetlana
2023.
On the main scientific achievements of Victor Selivanov.
Computability,
Vol. 12,
Issue. 4,
p.
301.
FOX, ALEC
2024.
COMPUTABLE PRESENTATIONS OF C*-ALGEBRAS.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 3,
p.
1313.
de Brecht, Matthew
Kihara, Takayuki
and
Selivanov, Victor
2024.
Ideal presentations and numberings of some classes of effective quasi-Polish spaces.
Computability,
p.
1.
Harrison-Trainor, Matthew
and
Melnikov, Alexander
2024.
An arithmetic analysis of closed surfaces.
Transactions of the American Mathematical Society,
Bazhenov, Nikolay
Melnikov, Alexander
and
Ng, Keng Meng
2024.
Every Δ⁰₂ Polish space is computable topological.
Proceedings of the American Mathematical Society,
Kornev, Ruslan
2024.
Twenty Years of Theoretical and Practical Synergies.
Vol. 14773,
Issue. ,
p.
405.
Ben-Shahar, Sapir
and
Koh, Heer Tern
2025.
Comparing notions of presentability in Polish spaces and Polish groups.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 5,
p.
103564.
Bagaviev, Ramil
Batyrshin, Ilnur I.
Bazhenov, Nikolay
Bushtets, Dmitry
Dorzhieva, Marina
Koh, Heer Tern
Kornev, Ruslan
Melnikov, Alexander G.
and
Ng, Keng Meng
2025.
Computably and punctually universal spaces.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 1,
p.
103491.
KOH, HEER TERN
MELNIKOV, ALEXANDER G.
and
NG, KENG MENG
2025.
COUNTEREXAMPLES IN EFFECTIVE TOPOLOGY.
The Journal of Symbolic Logic,
p.
1.
KOH, HEER TERN
MELNIKOV, ALEXANDER G.
and
NG, KENG MENG
2025.
COMPUTABLE TOPOLOGICAL GROUPS.
The Journal of Symbolic Logic,
Vol. 90,
Issue. 1,
p.
188.
Amir, Djamel Eddine
and
Hoyrup, Mathieu
2025.
Descriptive complexity of topological invariants.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 8,
p.
103611.
Badaev, Serikzhan
Bazhenov, Nikolay
Goncharov, Sergey
Kalmurzayev, Birzhan
and
Melnikov, Alexander
2025.
A non-computable c.e. closed subset of [0,1].
Journal of Logic and Computation,
Vol. 35,
Issue. 6,