Article contents
CONSERVATION THEOREMS ON SEMI-CLASSICAL ARITHMETIC
Published online by Cambridge University Press: 17 March 2022
Abstract
We systematically study conservation theorems on theories of semi-classical arithmetic, which lie in-between classical arithmetic 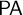 $\mathsf {PA}$ and intuitionistic arithmetic
$\mathsf {PA}$ and intuitionistic arithmetic 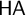 $\mathsf {HA}$. Using a generalized negative translation, we first provide a structured proof of the fact that
$\mathsf {HA}$. Using a generalized negative translation, we first provide a structured proof of the fact that 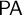 $\mathsf {PA}$ is
$\mathsf {PA}$ is 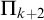 $\Pi _{k+2}$-conservative over
$\Pi _{k+2}$-conservative over 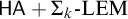 $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$ where
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$ where 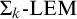 ${\Sigma _k}\text {-}\mathrm {LEM}$ is the axiom scheme of the law-of-excluded-middle restricted to formulas in
${\Sigma _k}\text {-}\mathrm {LEM}$ is the axiom scheme of the law-of-excluded-middle restricted to formulas in 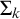 $\Sigma _k$. In addition, we show that this conservation theorem is optimal in the sense that for any semi-classical arithmetic T, if
$\Sigma _k$. In addition, we show that this conservation theorem is optimal in the sense that for any semi-classical arithmetic T, if 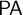 $\mathsf {PA}$ is
$\mathsf {PA}$ is 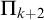 $\Pi _{k+2}$-conservative over T, then
$\Pi _{k+2}$-conservative over T, then 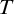 ${T}$ proves
${T}$ proves 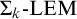 ${\Sigma _k}\text {-}\mathrm {LEM}$. In the same manner, we also characterize conservation theorems for other well-studied classes of formulas by fragments of classical axioms or rules. This reveals the entire structure of conservation theorems with respect to the arithmetical hierarchy of classical principles.
${\Sigma _k}\text {-}\mathrm {LEM}$. In the same manner, we also characterize conservation theorems for other well-studied classes of formulas by fragments of classical axioms or rules. This reveals the entire structure of conservation theorems with respect to the arithmetical hierarchy of classical principles.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by


