Article contents
THE CONSISTENCY STRENGTH OF LONG PROJECTIVE DETERMINACY
Published online by Cambridge University Press: 18 November 2019
Abstract
We determine the consistency strength of determinacy for projective games of length ω2. Our main theorem is that 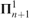 $\Pi _{n + 1}^1 $-determinacy for games of length ω2 implies the existence of a model of set theory with ω + n Woodin cardinals. In a first step, we show that this hypothesis implies that there is a countable set of reals A such that Mn (A), the canonical inner model for n Woodin cardinals constructed over A, satisfies
$\Pi _{n + 1}^1 $-determinacy for games of length ω2 implies the existence of a model of set theory with ω + n Woodin cardinals. In a first step, we show that this hypothesis implies that there is a countable set of reals A such that Mn (A), the canonical inner model for n Woodin cardinals constructed over A, satisfies 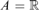 $$A = R$$ and the Axiom of Determinacy. Then we argue how to obtain a model with ω + n Woodin cardinal from this.
$$A = R$$ and the Axiom of Determinacy. Then we argue how to obtain a model with ω + n Woodin cardinal from this.
We also show how the proof can be adapted to investigate the consistency strength of determinacy for games of length ω2 with payoff in 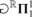 $^R R\Pi _1^1 $ or with σ-projective payoff.
$^R R\Pi _1^1 $ or with σ-projective payoff.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 3
- Cited by

