Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T06:51:48.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting finite models

Published online by Cambridge University Press:  12 March 2014

Alan R. Woods
Alan R. Woods*
Affiliation:
Department of Mathematics, University of Western Australia, Nedlands W.A. 6907, Australia, E-mail: woods@maths.uwa.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Let φ be a monadic second order sentence about a finite structure from a class 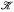which is closed under disjoint unions and has components. Compton has conjectured that if the number of n element structures has appropriate asymptotics, then unlabelled (labelled) asymptotic probabilities ν(φ) (μ(φ) respectively) for φ always exist. By applying generating series methods to count finite models, and a tailor made Tauberian lemma, this conjecture is proved under a mild additional condition on the asymptotics of the number of single component 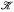-structures. Prominent among examples covered, are structures consisting of a single unary function (or partial function) and a fixed number of unary predicates.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 3 , September 1997 , pp. 925 - 949
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bender, E. A., Asymptotic methods in enumeration, SIAM Review, vol. 16 (1974), pp. 485–515.CrossRefGoogle Scholar
[2]Blass, A., Gurevich, Y., and Kozen, D., A zero-one law for logic with a fixed point operator, Information and Control, vol. 67 (1985), pp. 70–90.CrossRefGoogle Scholar
[3]Compton, K. J., Application of a Tauberian theorem to finite model theory, Arch. Math. Logik Grundlag, vol. 25 (1985), pp. 91–98.CrossRefGoogle Scholar
[4]Compton, K. J., A logical approach to asymptotic combinatorics I: first order properties, Advances in Mathematics, vol. 65 (1987), pp. 65–96.CrossRefGoogle Scholar
[5]Compton, K. J., Some methods for computing component distribution probabilities in relational structures, Discrete Mathematics, vol. 66 (1987), pp. 59–77.CrossRefGoogle Scholar
[6]Compton, K. J., A logical approach to asymptotic combinatorics II: monadic second-order properties, Journal of Combinatorial Theory. Series A, vol. 50 (1989), pp. 110–131.CrossRefGoogle Scholar
[7]Compton, K. J., Henson, C. W., and Shelah, S., Nonconvergence, undecidability, and intractability in asymptotic problems, Annals of Pure and Applied Logic, vol. 36 (1987), pp. 207–224.CrossRefGoogle Scholar
[8]Ebbinghaus, H.-D. and Flum, J., Finite model theory, Springer-Verlag, Berlin, 1995.Google Scholar
[9]Ehrenfeucht, A., An application of games to the completeness problem for formalized theories, Fundamenta Mathematicae, vol. 49 (1961), pp. 129–141.CrossRefGoogle Scholar
[10]Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 50–58.Google Scholar
[11]Feller, W., Introduction to probability theory and its applications, vol. 2, Wiley, New York, 1971.Google Scholar
[12]Fisher, R. A., Some combinatorial theorems and enumerations connected with the numbers of diagonal types of a latin square, Annals of Eugenics, vol. 11 (1942), pp. 395–401.CrossRefGoogle Scholar
[13]Fisher, R. A., Collected papers of R. A. Fisher (Bennett, J. H., editor), University of Adelaide, 1974.Google Scholar
[14]Foy, J. and Woods, A., Asymptotic number of nonisomorphic finite models with function symbols (preliminary report), Abstracts of the American Mathematical Society, vol. 843-03-85 (1988), p. 238.Google Scholar
[15]Foy, J. and Woods, A. R., Probabilities of sentences about two linear orderings, Feasible mathematics. A Mathematical Sciences Institute Workshop, Ithaca, New York, June 1989 (Buss, S. R. and Scott, P. J., editors), Birkhäuser, Boston, 1990, pp. 181–193.CrossRefGoogle Scholar
[16]Foy, J. M., Probability and enumeration results in the theory of finite models, Ph.D. thesis, Yale University, New Haven CT, 1994.Google Scholar
[17]Fraïssé, R., Sur quelques classifications des systèmes de relations, Pub. Sri. Univ. Alger. Ser. A., vol. 1 (1954), pp. 35–182.Google Scholar
[18]Freese, R., On the two kinds of probability in algebra, Algebra Universalis, vol. 27 (1990), pp. 70–79.CrossRefGoogle Scholar
[19]Glebskiǐ, Y. V., Kogan, D. I., Liogon'kiǐ, M. I., and Talanov, V. A., Range and degree of readability of formulas in the restricted predicate calculus, Kibernetika (Kiev), vol. 5 (1969), no. 2, pp. 17–28, English translation Cybernetics, vol. 5 (1972), pp. 142–154.Google Scholar
[20]Goulden, I. P. and Jackson, D. M., Combinatorial enumeration, Wiley, New York, 1983.Google Scholar
[21]Gurevich, Y., Monadic second-order theories, Model-theoretic logics (Barwise, J. and Feferman, S., editors), Springer-Verlag, New York, 1985, pp. 479–506.Google Scholar
[22]Harary, F., The number of functional digraphs, Mathematische Annalen, vol. 138 (1959), pp. 203–210.CrossRefGoogle Scholar
[23]Harary, F. and Palmer, E. M., Graphical enumeration, Academic Press, New York, 1973.Google Scholar
[24]Katz, L., Probability of indecomposability of a random mapping function, Annals of Mathematical Statistics, vol. 26 (1955), pp. 512–517.CrossRefGoogle Scholar
[25]Kaufmann, M. and Shelah, S., On random models of finite power and monadic logic, Discrete Mathematics, vol. 54 (1985), pp. 285–293.CrossRefGoogle Scholar
[26]Lynch, J. F., Probabilities of first-order sentences about unary functions, Transactions of the American Mathematical Society, vol. 287 (1985), pp. 543–568.CrossRefGoogle Scholar
[27]Lynch, J. F., Convergence laws for random words, Australian Journal of Combinatorics, vol. 7 (1993), pp. 145–156.Google Scholar
[28]Lynch, J. F., An extension of 0-1 laws, Random Structures Algorithms, vol. 5 (1994), pp. 155–172.CrossRefGoogle Scholar
[29]Meir, A. and Moon, J. W., On random mapping patterns, Combinatorica, vol. 4 (1984), pp. 61–70.CrossRefGoogle Scholar
[30]Meir, A., Some asymptotic results useful in enumeration problems, Aequationes Mathematicae, vol. 33 (1987), pp. 260–268.CrossRefGoogle Scholar
[31]Moon, J. W., Counting labelled trees, Canadian Mathematical Monographs, vol. 1, Canadian Mathematical Congress, 1970.Google Scholar
[32]Otter, R., The number of trees, Annals of Mathematics, vol. 49 (1948), pp. 583–599.CrossRefGoogle Scholar
[33]Pólya, G., Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen, Acta Mathematica, vol. 68 (1937), pp. 145–254.CrossRefGoogle Scholar
[34]Pólya, G. and Read, R. C., Combinatorial enumeration of groups, graphs, and chemical compounds, Springer-Verlag, New York, 1987.CrossRefGoogle Scholar
[35]Read, R.C., A note on the number of functional digraphs, Mathematische Annalen, vol. 143 (1961), pp. 109–110.CrossRefGoogle Scholar
[36]Rényi, A., On connected graphs, I, Publ. Math. Inst. Hung. Acad. Sci., vol. 4 (1959), pp. 385–388.Google Scholar
[37]Shelah, S., The monadic theory of order, Annals of Mathematics, vol. 102 (1975), pp. 379–419.CrossRefGoogle Scholar
[38]Spencer, J., Nonconvergence in the theory of random orders, Order, vol. 7 (1990/1991), pp. 341–348.Google Scholar
[39]Talanov, V. A. and Knyazev, V. V., The asymptotic truth value of infinite formulas, Proceedings of the all-Union seminar on discrete mathematics and its applications (Moscow 1984), Moskov. Gos. Univ., Mekh. Mat. Fak., Moscow, 1986, in Russian, MR 89g:03054, pp. 56–61.Google Scholar
[40]Tyszkiewicz, J., Infinitary queries and their asymptotic probabilities I: properties definable in transitive closure logic, Computer science logic. proc. 5th workshop, CSL'91 Berne Switzerland, October 1991 (Borger, E., Jäger, G., Büning, H. Klein, and Richter, M. M., editors), Lecture Notes in Computer Science, vol. 626, Springer-Verlag, 1992, pp. 396–410.CrossRefGoogle Scholar
[41]Tyszkiewicz, J., On asymptotic probabilities of monadic second order properties, Computer science logic. proc. 6th workshop, CSL'92 San Miniato, 1992 (Borger, E., Jäger, G., Büning, H. Klein, Martini, S., and Richter, M. M., editors), Lecture Notes in Computer Science, vol. 702, Springer-Verlag, 1993, pp. 425–439.Google Scholar
[42]Tyszkiewicz, J., Infinitary queries and their asymptotic probabilities, II. Properties definable in least fixed point logic, Random Structures Algorithms, vol. 5 (1994), pp. 215–234.CrossRefGoogle Scholar
[43]Tyszkiewicz, J., Probabilities in first-order logic of a unary function and a binary relation, Random Structures Algorithms, vol. 6 (1995), pp. 181–192.CrossRefGoogle Scholar
[44]Wilf, H. S., generatingfunctionology, Academic Press, Boston, 1990.Google Scholar
[45]Woods, A. R., Colouring rules for finite trees, and probabilities of monadic second order sentences, Research Report 15, Department of Mathematics, University of Western Australia, 1995.Google Scholar