Article contents
Creativeness and completeness in recursion categories of partial recursive operators
Published online by Cambridge University Press: 12 March 2014
Extract
Recursion categories have been proposed by Di Paola and Heller in [DPH] as the basis for a category-theoretic approach to recursion theory, in the context of a more general and ambitious project of a purely algebraic treatment of incompleteness phenomena. The way in which the classical notion of creative set is rendered in this new category-theoretic framework plays, therefore, a central role. This is done in [DPH] (Definition 8.1) by defining the notion of creative domains or, rather, domains which are creative relative to some criterion: thus, in a recursion category, every criterion provides a notion of creativeness.
A basic result on creative domains (cf. [DPH, Theorem 8.13]) is that, under certain assumptions, a version of the classical result, due to Myhill [MYH], stating that every creative set is complete, holds: in a recursion category with equality (i.e. 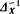 exists for every object X) and having enough atoms, every domain which is creative with respect to atoms is also complete.
exists for every object X) and having enough atoms, every domain which is creative with respect to atoms is also complete.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 3
- Cited by

