Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-14T23:51:33.816Z Has data issue: false hasContentIssue false
  • English
  • Français

Cuts in hyperfinite time lines

Published online by Cambridge University Press:  12 March 2014

Renling Jin
Renling Jin*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Abstract

In an ω1-saturated nonstandard universe a cut is an initial segment of the hyperinlegers which is closed under addition. Keisler and Leth in [KL] introduced, for each given cut U, a corresponding U-topology on the hyperintegers by letting O be U-open if for any x ϵ O there is a y greater than all the elements in U such that the interval [x − y, x + y] ⊆ O. Let U be a cut in a hyperfinite time line 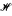, which is a hyperfinite initial segment of the hyperintegers. U is called a good cut if there exists a U-meager subset of 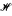of Loeb measure one. Otherwise U is bad. In this paper we discuss the questions of Keisler and Leth about the existence of bad cuts and related cuts. We show that assuming b > ω1, every hyperfinite time line has a cut with both cofinality and coinitiality uncountable. We construct bad cuts in a nonstandard universe under ZFC. We also give two results about the existence of other kinds of cuts.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 2 , June 1992 , pp. 522 - 527
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ca]Canjar, M., Countable ultraproducts without CH, Annals of Pure and Applied Logic, vol. 37 (1988), pp. 1–79.CrossRefGoogle Scholar
[CK]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973; 3rd ed., 1990.Google Scholar
[KKML]Keisler, H. J., Kunen, K., Miller, A. W., and Leth, S., Descriptive set theory over hyperfinite sets, this Journal, vol. 54 (1989), pp. 1167–1180.Google Scholar
[KL]Keisler, H. J. and Leth, S., Meager sets on the hyperfinite time line, this Journal, vol. 56 (1991), pp. 71–102.Google Scholar
[Lo]Loeb, P., Conversion from nonstandard to standard measure space and applications in probability theory, Transactions of the American Mathematical Society, vol. 211 (1975), pp. 113–122.CrossRefGoogle Scholar
[SB]Stroyan, K. D. and Bayod, J. M., Foundations of infinitesimal stochastic analysis, North-Holland, Amsterdam, 1986.Google Scholar