Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-14T08:51:33.548Z Has data issue: false hasContentIssue false
  • English
  • Français

Degrees coded in jumps of orderings

Published online by Cambridge University Press:  12 March 2014

Julia F. Knight
Julia F. Knight*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801
*
Department of Mathematics, University of Notre Dame, Notre Dame, Indiana 46556
Get access Rights & Permissions [Opens in a new window]

Extract

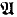All structures to be considered here have universe ω, and all languages come equipped with Gödel numberings. If is a structure, then D(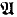), the open diagram of 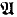, can be thought of as a subset of ω, and it makes sense to talk about the Turing degree deg(D(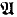)). This depends on the presentation as well as the isomorphism type of .

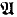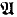For example, consider the ordering = (ω, <). For any B ⊆ ω, it is possible to code B in a copy of 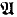as follows: Let π be the permutation of ω such that for each n ∈ ω, π leaves 2n and 2n + 1 fixed if n ∈ B and switches 2n with 2n + 1 if n ∉ B. Let 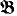be the copy of 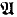such that 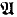≃π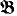. Then n ∈ B iff the sentence 2n < 2n + 1 is in D(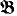). In §4, this idea will be used to show that for any structure 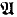that is not completely trivial, {deg(D(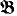)): 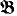≃ 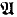} is closed upwards.

It would be satisfying to have a way of assigning Turing degrees to structures such that the degree assigned to a given structure measured the recursion-theoretic complexity of the isomorphism type and was independent of the presentation. Jockusch suggested the following.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 4 , December 1986 , pp. 1034 - 1042
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Jockusch, C. and Soare, R., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[2]Läuchli, H., A decision procedure for the weak second order theory of linear order, Contributions to mathematical logic (colloquium, Hannover, 1966), North-Holland, Amsterdam, 1968, pp. 189–197.CrossRefGoogle Scholar
[3]Marker, D., Degree of models of true arithmetic, Proceedings of the Herbrand symposium, (Marseille, 1981; Stern, J., editor), North-Holland, Amsterdam, 1982, pp. 233–242.Google Scholar
[4]Richter, Linda Jean, Degrees of structures, this Journal, vol. 46 (1981), pp. 723–731.Google Scholar
[5]Rosenstein, J., Linear orderings, Academic Press, New York, 1982.Google Scholar
[6]Rubin, M., Theories of linear order, Israel Journal of Mathematics, vol. 17 (1974), pp. 392–443.CrossRefGoogle Scholar
[7]Scott, D., Invariant Borel sets, Fundamenta Mathematicae, vol. 56 (1964), pp. 117–128.CrossRefGoogle Scholar
[8]Selman, A., Applications of forcing to the degree theory of the arithmetic hierarchy, Proceedings of the London Mathematical Society, ser. 3, vol. 25 (1972), pp. 586–602.CrossRefGoogle Scholar