Article contents
Differentially algebraic group chunks
Published online by Cambridge University Press: 12 March 2014
Extract
We point out that a group first order definable in a differentially closed field K of characteristic 0 can be definably equipped with the structure of a differentially algebraic group over K. This is a translation into the framework of differentially closed fields of what is known for groups definable in algebraically closed fields (Weil's theorem).
I restrict myself here to showing (Theorem 20) how one can find a large “differentially algebraic group chunk” inside a group defined in a differentially closed field. The rest of the translation (Theorem 21) follows routinely, as in [B].
What is, perhaps, of interest is that the proof proceeds at a completely general (soft) model theoretic level, once Facts 1–4 below are known.
Fact 1. The theory of differentially closed fields of characteristic 0 is complete and has quantifier elimination in the language of differential fields (+, ·,0,1, −1,d).
Fact 2. Affine n-space over a differentially closed field is a Noetherian space when equipped with the differential Zariski topology.
Fact 3. If K is a differentially closed field, k ⊆ K a differential field, and a and 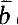 are in k, then a is in the definable closure of k ◡
are in k, then a is in the definable closure of k ◡ 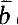 iff a ∈ ‹
iff a ∈ ‹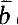 › (where k ‹
› (where k ‹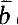 › denotes the differential field generated by k and
› denotes the differential field generated by k and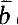 ).
).
Fact 4. The theory of differentially closed fields of characteristic zero is totally transcendental (in particular, stable).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 6
- Cited by

