Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bell, J. L.
1974.
On Compact Cardinals.
Mathematical Logic Quarterly,
Vol. 20,
Issue. 25-27,
p.
389.
1974.
Set Theory - An Introduction to Large Cardinals.
Vol. 76,
Issue. ,
p.
319.
Boos, William
1975.
⊨ISILC Logic Conference.
Vol. 499,
Issue. ,
p.
25.
Galvin, Fred
and
Prikry, Karel
1976.
Infinitary jonsson algebras and partition relations.
Algebra Universalis,
Vol. 6,
Issue. 1,
p.
367.
1977.
Logic Colloquium 76, Proceedings of a conference.
Vol. 87,
Issue. ,
p.
567.
Wang, Hao
1977.
Logic, Foundations of Mathematics, and Computability Theory.
p.
309.
1977.
HANDBOOK OF MATHEMATICAL LOGIC.
Vol. 90,
Issue. ,
p.
371.
Kanamori, A.
and
Magidor, M.
1978.
Higher Set Theory.
Vol. 669,
Issue. ,
p.
99.
Solovay, Robert M.
Reinhardt, William N.
and
Kanamori, Akihiro
1978.
Strong axioms of infinity and elementary embeddings.
Annals of Mathematical Logic,
Vol. 13,
Issue. 1,
p.
73.
1978.
Logic Colloquium '77.
Vol. 96,
Issue. ,
p.
145.
1978.
Vol. 79,
Issue. ,
p.
596.
Tall, Franklin D.
1980.
Surveys in General Topology.
p.
445.
1982.
Logic Colloquium '80 - Papers intended for the European Summer Meeting of the Association for Symbolic Logic.
Vol. 108,
Issue. ,
p.
173.
Drake, F. R.
1985.
How recent work in mathematical logic relates to the foundations of mathematics.
The Mathematical Intelligencer,
Vol. 7,
Issue. 4,
p.
27.
Laver, Richard
1992.
The left distributive law and the freeness of an algebra of elementary embeddings.
Advances in Mathematics,
Vol. 91,
Issue. 2,
p.
209.
Shioya, Masahiro
1994.
Infinitary J�nsson functions and elementary embeddings.
Archive for Mathematical Logic,
Vol. 33,
Issue. 2,
p.
81.
Zapletal, Jindrich
1996.
A new proof of Kunen’s inconsistency.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 7,
p.
2203.
Jech, Thomas
1997.
Large Ordinals.
Advances in Mathematics,
Vol. 125,
Issue. 2,
p.
155.
Laver, Richard
1997.
Implications between strong large cardinal axioms.
Annals of Pure and Applied Logic,
Vol. 90,
Issue. 1-3,
p.
79.
Maddy, Penelope
2000.
The Growth of Mathematical Knowledge.
p.
341.

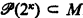 , then
, then 