Article contents
ELIMINATION OF IMAGINARIES IN ORDERED ABELIAN GROUPS WITH BOUNDED REGULAR RANK
Published online by Cambridge University Press: 06 February 2023
Abstract
In this paper we study elimination of imaginaries in some classes of pure ordered abelian groups. For the class of ordered abelian groups with bounded regular rank (equivalently with finite spines) we obtain weak elimination of imaginaries once we add sorts for the quotient groups 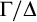 $\Gamma /\Delta $ for each definable convex subgroup
$\Gamma /\Delta $ for each definable convex subgroup 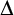 $\Delta $, and sorts for the quotient groups
$\Delta $, and sorts for the quotient groups 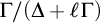 $\Gamma /(\Delta + \ell \Gamma )$ where
$\Gamma /(\Delta + \ell \Gamma )$ where 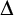 $\Delta $ is a definable convex subgroup and
$\Delta $ is a definable convex subgroup and 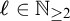 $\ell \in \mathbb {N}_{\geq 2}$. We refer to these sorts as the quotient sorts. For the dp-minimal case we obtain a complete elimination of imaginaries if we also add constants to distinguish the cosets of
$\ell \in \mathbb {N}_{\geq 2}$. We refer to these sorts as the quotient sorts. For the dp-minimal case we obtain a complete elimination of imaginaries if we also add constants to distinguish the cosets of 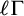 $\ell \Gamma $ in
$\ell \Gamma $ in 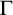 $\Gamma $, where
$\Gamma $, where 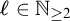 $\ell \in \mathbb {N}_{\geq 2}$.
$\ell \in \mathbb {N}_{\geq 2}$.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 2
- Cited by


