Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T17:46:56.906Z Has data issue: false hasContentIssue false
  • English
  • Français

The entire NS ideal on 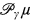can be precipitous

Published online by Cambridge University Press:  12 March 2014

Noa Goldring
Noa Goldring*
Affiliation:
Department of Mathematics, Occidental College, Los Angeles, California 90041, USA, E-mail: goldring@oxy.edu
Get access Rights & Permissions [Opens in a new window]

Extract

The main result of this note is showing that if γ and μ are regular uncountable cardinals with γ ≤ μ then the non-stationary ideal (henceforth the NS ideal) on 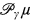can be precipitous. This strengthens a result of [1] showing, under the same hypotheses, that a restriction of this ideal can be precipitous. See [1, Theorem 29, p. 36]. In fact, we show that even the strongly NS ideal on 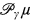is precipitous in our model (since the former ideal is a restriction of the latter, the latter's being precipitous is a stronger assertion).

More precisely, by starting with a model of “ZFC + ‘κ is a supercompact cardinal’ + ‘μ < κ is a regular uncountable cardinal’ ”, we generate a model of ZFC where all cardinals below and including μ are not collapsed and where the NS and strongly NS ideals on Pγμ are precipitous, for all regular uncountable γ which are less than or equal to μ.

As far as consistency strength, we can obtain the same result even if κ is only Woodin in the ground model. However, the proof of this result is more complicated than in the case when κ is a supercompact cardinal. Furthermore, there are essentially no new ideas in adapting the proof relative to a supercompact cardinal to that relative to a Woodin cardinal beyond what appears in, e.g., [2]. We therefore give the complete proof relative to the existence of a supercompact cardinal and then briefly sketch the proof relative to the existence of a Woodin cardinal, using [2] as a reference.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 4 , December 1997 , pp. 1161 - 1172
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Foreman, M., Magidor, M., and Shelah, S., Martin's maximum, saturated ideals and non-regular ultrafilters, Part I, Annals of Mathematics, vol. 127 (1988), pp. 1–47.CrossRefGoogle Scholar
[2]Goldring, N., Woodin cardinals and presaturated ideals, Annals of Pure and Applied Logic, vol. 55 (1992), pp. 285–303.CrossRefGoogle Scholar
[3]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[4]Kueker, D. W., Countable approximations and Löwenheim-Skolem theorems, Annals of Mathematical Logic, vol. 11 (1977), no. 1, pp. 57–103.CrossRefGoogle Scholar
[5]Martin, D. A., Borel and projective determinacy, book to be published.Google Scholar
[6]Martin, D. A. and Steel, J. R., A proof of projective determinacy, Journal of the American Mathematical Society, vol. 2 (1989), pp. 71–125.CrossRefGoogle Scholar