Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T19:07:42.095Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental logics and Π30 theories1

Published online by Cambridge University Press:  12 March 2014

Petr Hájek
Petr Hájek*
Affiliation:
Czechoslovak Academy of Sciences, 115 67 Prague, Czechoslovakia
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we are going to consider experimental logics introduced by Jeroslow [4] as models of human reasoning proceeding by trial and error, i.e. admitting changes of axioms in time (some axioms are deleted, some new ones accepted). Jeroslow's notion is based on the idea that events which may cause changes in axioms and rules of reasoning are mechanical. Suppose a finite alphabet Γ to be fixed and let Γ* be the set of words in the alphabet Γ. N denotes the set of natural numbers.

0.1. Definition. An experimental logic is a recursive relation H ⊆ N × Γ*; H(t, φ) is read “the expression is accepted at the point of time t”. φ is recurring w.r.t. H (notation: RecH(φ)) if H(t, φ) holds for infinitely many t; is stable w.r.t. H (notation: StblH(φ)) if H(t,φ) holds for all but finitely many t. In symbols:

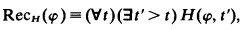
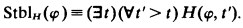
H is convergent if every recurring expression is stable.

0.2. We have the following facts: Let X ∈ Γ*. (1) X ∈ 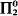iff there is an experimental logic H such that X = {φ; RecH(φ)}- (2) X ∈ iff there is an experimental logic H such that X = {φ; StblH(φ)}. (3) X ∈ 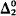iff there is a convergent experimental logic H such that X is the set of all expressions recurring ( = stable) w.r.t. H. (See [4], [3], [7]; cf. also [5].)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 4 , December 1977 , pp. 515 - 522
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Thanks are due to Professor R. G. Jeroslow for correspondence which has been very helpful in preparing the present paper. The results of this paper were presented at the conference on Mathematical Logic at the Mathematisches Forschungsinstitut Oberwolfach on April 12, 1976. Thanks are due to Professors G. H. Müller and E. P. Specker for valuable comments. I am grateful to my wife M. Hájková who read the manuscript and detected various mistakes and to F. N. Springsteel who proofread the English.

References

REFERENCES

[1]Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49(1960), pp. 35–92.CrossRefGoogle Scholar
[2]Feferman, S., Kreisel, G. and Orey, S., 1-consistency and faithful interpretations, Archiv für mathematische Logik, vol. 6(1972), pp. 52–63.CrossRefGoogle Scholar
[3]Gold, E. M., Limiting recursion, this Journal, vol. 30(1965), pp. 28–48.Google Scholar
[4]Jeroslow, R. G., Experimental logics and Δ20 theories, Journal of Philosophical Logic, vol. 4(1975), pp. 253–267.CrossRefGoogle Scholar
[5]Magari, R., Su certe teorie non denumerabili, Annali di Matematica Pura ed Applicant, vol. 48(1974), pp. 119–152.CrossRefGoogle Scholar
[6]Mostowski, A., Examples of sets definable by means of two and three quantifiers, Fundamenta Mathematicae, vol. 42 (1957), pp. 259–270.CrossRefGoogle Scholar
[7]Putnam, H., Trial and error predicates and the solution of a problem of Mostowski, this Journal, vol. 30(1965), pp. 49–57.Google Scholar
[8]Rabin, M. O., Non-standard models and independence of the induction axiom, Essays on the Foundations of Mathematics (in honor of A. A. Fraenkel), Jerusalem, 1961, pp. 287–299.Google Scholar
[9]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar