Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:46:03.661Z Has data issue: false hasContentIssue false
  • English
  • Français

FRAGMENTS OF APPROXIMATE COUNTING

Published online by Cambridge University Press:  25 June 2014

SAMUEL R. BUSS ,
LESZEK ALEKSANDER KOŁODZIEJCZYK  and
NEIL THAPEN
SAMUEL R. BUSS
Affiliation:
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF CALIFORNIA, SAN DIEGO, LA JOLLA, CA 92093-0112, USAE-mail:sbuss@math.ucsd.edu
LESZEK ALEKSANDER KOŁODZIEJCZYK
Affiliation:
INSTITUTE OF MATHEMATICS, UNIVERSITY OF WARSAW, BANACHA 2, 02-097 WARSZAWA, POLANDE-mail:lak@mimuw.edu.pl
NEIL THAPEN
Affiliation:
INSTITUTE OF MATHEMATICS, ACADEMY OF SCIENCES OF THE CZECH REPUBLIC, ŽITNÁ 25, 115 67 PRAHA 1, CZECH REPUBLICE-mail:thapen@math.cas.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

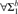We study the long-standing open problem of giving $\forall {\rm{\Sigma }}_1^b$ separations for fragments of bounded arithmetic in the relativized setting. Rather than considering the usual fragments defined by the amount of induction they allow, we study Jeřábek’s theories for approximate counting and their subtheories. We show that the 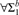$\forall {\rm{\Sigma }}_1^b$ Herbrandized ordering principle is unprovable in a fragment of bounded arithmetic that includes the injective weak pigeonhole principle for polynomial time functions, and also in a fragment that includes the surjective weak pigeonhole principle for FPNP functions. We further give new propositional translations, in terms of random resolution refutations, for the consequences of $T_2^1$ augmented with the surjective weak pigeonhole principle for polynomial time functions.

Keywords

Approximate countingbounded arithmeticordering principleweak pigeonhole principlerandom resolutionpolynomial local search
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 2 , June 2014 , pp. 496 - 525
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beckmann, A. and Buss, S., Polynomial local search in the polynomial hierarchy and witnessing in fragments of bounded arithmetic, Journal of Mathematical Logic, vol. 9 (2009), pp. 103–138.Google Scholar
Beckmann, A. and Buss, S., Characterization of definable search problems in bounded arithmetic via proof notations, Ways of Proof Theory, Ontos Verlag, Frankfurt 2010, pp. 65–134.Google Scholar
Ben-Sasson, E. and Wigderson, A., Short proofs are narrow—resolution made simple, Journal of the ACM, vol. 48 (2001), pp. 149–169.CrossRefGoogle Scholar
Boughattas, S. and Kołodziejczyk, L. A., The strength of sharply bounded induction requires MSP, Annals of Pure and Applied Logic, vol. 161 (2010), pp. 504–510.CrossRefGoogle Scholar
Buss, S., Bounded Arithmetic, Bibliopolis, Napoli 1986.Google Scholar
Buss, S., Axiomatizations and conservation results for fragments of bounded arithmetic, In Logic and Computation, Proceedings of a workshop held at Carnegie Mellon University, American Mathematical Society, 1990, pp. 57–84.CrossRefGoogle Scholar
Buss, S., First-order proof theory of arithmetic, In Handbook of Proof Theory (Buss, S., editor), Elsevier, Amsterdam 1998, pp. 79–147.Google Scholar
Buss, S. and Krajíček, J., An application of Boolean complexity to separation problems in bounded arithmetic, Proceedings of the London Mathematical Society, vol. 69 (1994), pp. 1–21.CrossRefGoogle Scholar
Chiari, M. and Krajíček, J., Witnessing functions in bounded arithmetic and search problems, this Journal, vol. 63 (1998), pp. 1095–1115.Google Scholar
Chiari, M. and Krajíček, J., Lifting independence results in bounded arithmetic, Archive for Mathematical Logic, vol. 38 (1999), pp. 123–138.Google Scholar
Hájek, P. and Pudlák, P., The Metamathematics of First Order Arithmetic, Springer, Berlin 1993.CrossRefGoogle Scholar
Jeřábek, E., Dual weak pigeonhole principle, Boolean complexity, and derandomization, Annals of Pure and Applied Logic, vol. 129 (2004), pp. 1–37.Google Scholar
Jeřábek, E., The strength of sharply bounded induction, Mathematical Logic Quarterly, vol. 52 (2006), pp. 613–624.CrossRefGoogle Scholar
Jeřábek, E., Approximate counting in bounded arithmetic, this Journal, vol. 72 (2007), pp. 959–993.Google Scholar
Jeřábek, E., On independence of variants of the weak pigeonhole principle, Journal of Logic and Computation, vol. 17 (2007), pp. 587–604.Google Scholar
Jeřábek, E., Approximate counting by hashing in bounded arithmetic, this Journal, vol. 74 (2009), pp. 829–860.Google Scholar
Kołodziejczyk, L. A., Nguyen, P., and Thapen, N., The provably total NP search problems of weak second-order bounded arithmetic, Annals of Pure and Applied Logic, vol. 162 (2011), pp. 419–446.Google Scholar
Krajíček, J., No counter-example interpretation and interactive computation, In Logic from Computer Science (Moschovakis, Y., editor), vol. 21 (1992), Mathematical Sciences Research Institute Publications, Springer, Berlin pp. 287–293.Google Scholar
Krajíček, J., Lower bounds to the size of constant-depth propositional proofs, this Journal, vol. 59 (1994), pp. 73–86.Google Scholar
Krajíček, J., Bounded Arithmetic, Propositional Logic and Computational Complexity, Cambridge University Press, 1995.Google Scholar
Krajíček, J., On the weak pigeonhole principle, Fundamenta Mathematicae, vol. 170 (2001),pp. 123–140.Google Scholar
Krajíček, J., Pudlák, P., and Takeuti, G., Bounded arithmetic and the polynomial hierarchy, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 143–153.Google Scholar
Lauria, M., Short Res*(polylog) refutations if and only if narrow Res refutations, 2011, available at arXiv:1310.5714.Google Scholar
Maciel, A., Pitassi, T., and Woods, A., A new proof of the weak pigeonhole principle, Proceedings of the 32nd Annual ACM Symposium on Theory of Computing, 2000, pp. 368–377.Google Scholar
Parikh, R., Existence and feasibility in arithmetic, this Journal, vol. 36 (1971), pp. 494–508.Google Scholar
Paris, J., Wilkie, A., and Woods, A., Provability of the pigeonhole principle and the existence of infinitely many primes, this Journal, vol. 53 (1988), pp. 1235–1244.Google Scholar
Pudlák, P., Ramsey’s theorem in bounded arithmetic, In Computer Science Logic: Proceedings of the 4th Workshop, CSL ’90 (Börger, E., Büning, H. Kleine, Richter, M., and Schönfeld, W., editors), Springer, Berlin 1991, pp. 308–317.Google Scholar
Pudlák, P., Some relations between subsystems of arithmetic and the complexity of computations, Logic From Computer Science: Proceedings of a Workshop held November 13-17, 1989, Mathematical Sciences Research Institute Publication #21, Springer-Verlag, Berlin 1992, pp. 499–519.Google Scholar
Pudlák, P., Consistency and games—in search of new combinatorial principles, In Logic Colloquium ’03 (Stoltenberg-Hansen, V. and Väänänen, J., editors), Lecture Notes in Logic, no. 24, Association of Symbolic Logic, 2006, pp. 244–281.CrossRefGoogle Scholar
Pudlák, P. and Thapen, N., Alternating minima and maxima, Nash equilibria and bounded arithmetic, Annals of Pure and Applied Logic, vol. 163 (2012), pp. 604–614.Google Scholar
Riis, S., Making infinite structures finite in models of second order bounded arithmetic, In Arithmetic, Proof Theory, and Computational Complexity (Clote, P. and Krajíček, J., editors), Oxford University Press, Oxford 1993, pp. 289–319.Google Scholar
Segerlind, N., Buss, S., and Impagliazzo, R., A switching lemma for small restrictions and lower bounds for k-DNF resolution, SIAM Journal on Computing, vol. 33 (2004), pp. 1171–1200.CrossRefGoogle Scholar
Skelley, A. and Thapen, N., The provably total search problems of bounded arithmetic, Proceedings of the London Mathematical Society, vol. 103 (2011), pp. 106–138.Google Scholar
Thapen, N., A model-theoretic characterization of the weak pigeonhole principle, Annals of Pure and Applied Logic, vol. 118 (2002), pp. 175–195.Google Scholar
Thapen, N., Structures interpretable in models of bounded arithmetic, Annals of Pure and Applied Logic, vol. 136 (2005), pp. 247–266.Google Scholar