Article contents
A further consistent extension of basic logic
Published online by Cambridge University Press: 12 March 2014
Extract
1.1. In two previous papers a consistent theory of real numbers has been outlined by the author, using a system K′. This latter system is an extension of a system K, which is “basic” in the sense that every finitary (recursively enumerable) subclass of its well-formed expressions is in a certain sense represented in it. The system L described below is a further extension of K. The system K′ lacks two important features possessed by L: a symbol for a special kind of implication (or “conditionality”) and a symbol for the modal concept “necessity.” The presence of the implication symbol, and the additional assumptions that go with it, make available in L various kinds of restricted universal quantification not available in K′, for example, universal quantification restricted to the real numbers of the author's theory of real numbers.
1.2. If ‘~[a & ~a]’ is a theorem of L, then the proposition expressed by ‘a’ may be said to L-satisfy the principle of excluded middle. I t is always the case that ‘a’ L-satisfies the principle of excluded middle (or rather that the proposition expressed by ‘a’ does so) if and only if ‘a’ or ‘~a’ is a theorem of L. An example of a proposition that does not L-satisfy the principle of excluded middle is that expressed by ‘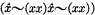 ’, namely the proposition that asserts that the class of classes that are not members of themselves is a member of itself.
’, namely the proposition that asserts that the class of classes that are not members of themselves is a member of itself.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1950
References
1 An extension of basic logic, this Journal vol. 13 (1948), pp. 95–106Google Scholar, and The Heine-Borel theorem in extended basic logic, ibid., vol. 14 (1949), pp. 9–15, See also by this writer: A basic logic, ibid., vol. 7 (1942), pp. 105–114, Representations of calculi, ibid., vol. 9 (1944), pp. 57–62, and A minimum calculus for logic, ibid., pp. 89–94. The use of “introduction” and “elimination” rules in the present paper was inspired by partly similar rules employed by Bernays, Paul in his Logical calculus (mimeographed, Princeton, 1936)Google Scholar, who in turn had been influenced by Gentzen, (Untersuchungen über das logische Schliessen, Mathematische Zeitschrift, vol. 39 (1934–1935), pp. 176–210, 405–431CrossRefGoogle Scholar) and Jaśkowski, (On the rules of suppositions in formal logic, Studia logica, no. 1, Warsaw, 1934)Google Scholar.
2 The implication symbol would also make it easier to formulate the theory of numbers of the writer's paper, On natural numbers, integers, and rationals, this Journal, vol. 14 (1949), pp. 81–84Google Scholar.
3 For a similar line of thought see pp. 16–18 of Church's, Alonzo mimeographed lectures entitled Mathematical logic (delivered at Princeton University, October 1935–01 1936)Google Scholar.
4 Heyting, A., Die formalen Regeln der intuitionistischen Logik, Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 1930, pp. 42–56Google Scholar; Die formalen Regeln der intuitionistischen Mathematik, ibid., pp. 57–71; On weakened quantification, this Journal, vol. 11 (1946), pp. 119–121.
5 This method is due to Curry, H. B. in his paper, The inconsistency of certain formal logics, this Journal, vol. 7 (1942), pp. 115–117Google Scholar.
6 See Appendix II of Lewis and Langford's, Symbolic logic (New York and London, 1932)Google Scholar. See also Barcan, Ruth C., A functional calculus of first order based on strict implication, this Journal, vol. 11 (1946), pp. 1–16Google Scholar, The deduction theorem in afunctional calculus of first order based on strict implication, ibid., pp. 115–118, and The identity of individuals in a strict functional calculus of second order, ibid., vol. 12 (1947), pp. 12–15. [Remarks added March 3, 1949: Mention might also be made of the writer's paper, Intuitionislic modal logic with quantifiers, forthcoming in Portugaliae mathematica. In connection with the present paper, it is probably worth noting that the system L was intentionally constructed in such a way that with very slight changes it could be converted from an S5 type of modal system to an S4 or S2 type. The change to an S4 type can be achieved by omitting the last sentences of 3.20 and 3.23 respectively. A further modification as follows then converts L into an S2 type: Replace the phrase beginning with “where” in 3.20 by the phrase, “where ‘b 1’, ‘b 2‘, …, are the members of Y.” The results of this paper are easily seen to remain valid when L is modified in either of these ways.]
- 3
- Cited by

