No CrossRef data available.
Article contents
Fusion of 2-elements in groups of finite Morley rank
Published online by Cambridge University Press: 12 March 2014
Extract
The Alperin-Goldschmidt Fusion Theorem [1, 5], when combined with pushing up [7], was a useful tool in the classification of the finite simple groups. Similar theorems are needed in the study of simple groups of finite Morley rank, in the even type case (that is, when the Sylow 2-subgroups are of bounded exponent, as in algebraic groups over fields of characteristic 2). In that context a body of results relating to fusion of 2-elements and the structure of 2-local subgroups is needed: pushing up, and the classification of groups with strongly or weakly embedded subgroups, or have strongly closed abelian subgroups (c.f, [2]). Two theorems of Alperin-Goldschmidt type are proved here. Both are needed in applications.
The following is an exact analog of the Alperin-Goldschmidt Fusion Theorem for groups of finite Morley rank, in the case of 2-elements:
Theorem 1.1. Let G be a group of finite Morley rank, and P a Sylow 2-subgroup of G. If A, B ⊆ P are conjugate in G, then there are subgroups Hi ≤ Pand elementsxi ∈ N(Hi) for 1 ≤ i ≤ n, and an elementy ∈ N(P), such that for all i:
1. Hi is a tame intersection of two Sylow 2-subgroups;
2. CP(Hi) ≤ Hi;
3. N(Hi)/Hiis 2-isolated
and
(a) 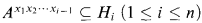
(b) 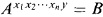 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001

