No CrossRef data available.
Article contents
Generalized interpolation theorems
Published online by Cambridge University Press: 12 March 2014
Extract
Chang [1], [2] has proved the following generalization of the Craig interpolation theorem [3]: For any first-order formulas φ and ψ with free first- and second-order variables among ν1, …, νn, R and ν1, …, νn, S respectively, and for any sequence Q1, …, Qn of quantifiers such that Q1 is universal whenever ν1 is a second-order variable, if
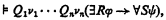
then there is a first-order formula θ with free variables among ν1, …, νn such that
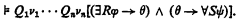
(Note that the Craig interpolation theorem is the special case of Chang's theorem in which Q1, …, Qn are all universal quantifiers.) Chang also raised the question [2, Remark (k)] as to whether the Lopez-Escobar interpolation theorem [6] for the infinitary language Lω1ω possesses a similar generalization. In this paper, we show that the answer to Chang's question is affirmative and, moreover, that several interpolation theorems for applied second-order languages for number theory also possess such generalizations.
Maehara and Takeuti [7] have established independently proof-theoretic interpolation theorems for first-order logic and Lω1ω which have as corollaries both Chang's theorem and its analog for Lω1ω. Our proofs are quite different from theirs and rely on model-theoretic techniques stemming from the analogy between the theory of definability in Lω1ω and the theory of Borel and analytic sets of real numbers, rather than the technique of cut-elimination.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972

