Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T18:28:08.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized nonsplitting in the recursively enumerable degrees

Published online by Cambridge University Press:  12 March 2014

Steven D. Leonhardi
Steven D. Leonhardi*
Affiliation:
Winona State University, Department of Mathematics and Statistics, Winona, MN 55987, USA, E-mail: leonhardi@vax2.winona.msus.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the algebraic structure of the upper semi-lattice formed by the recursively enumerable Turing degrees. The following strong generalization of Lachlan's Nonsplitting Theorem is proved: Given n ≥ 1, there exists an r.e. degree d such that the interval [d, 0′] ⊂ R admits an embedding of the n-atom Boolean algebra 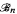preserving (least and) greatest element, but also such that there is no (n + 1 )-tuple of pairwise incomparable r.e. degrees above d which pairwise join to 0′ (and hence, the interval [d, 0′] ⊂ R does not admit a greatest-element-preserving embedding of any lattice 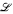which has n + 1 co-atoms, including 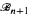). This theorem is the dual of a theorem of Ambos-Spies and Soare, and yields an alternative proof of their result that the theory of R has infinitely many one-types.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 2 , June 1997 , pp. 397 - 437
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ambos-Spies, K. and Lerman, M., Lattice embeddings into the recursively enumerable degrees, this Journal, vol. 51 (1986), pp. 257–272.Google Scholar
[2]Ambos-Spies, K., Lattice embeddings into the recursively enumerable degrees: II, this Journal, vol. 54 (1989), pp. 735–760.Google Scholar
[3]Ambos-Spies, K. and Shore, R. A., One-types and undecidability in the recursively enumerable degrees, Annals of Pure and Applied Logic, vol. 63 (1993), pp. 3–37.CrossRefGoogle Scholar
[4]Ambos-Spies, K. and Soare, R. I., The recursively enumerable degrees have infinitely many one-types, Annals of Pure and Applied Logic, vol. 44 (1989), pp. 1–23.CrossRefGoogle Scholar
[5]Cooper, S. B., Harrington, L., Lachlan, A. H., Lempp, S., and Soare, R. I., The d.r.e. degrees are not dense, Annals of Pure and Applied Logic, vol. 55 (1991), pp. 125–151.CrossRefGoogle Scholar
[6]Fejer, P. A., Branching degrees above low degrees, Transactions of the American Mathematical Society, vol. 273 (1982), pp. 157–180.CrossRefGoogle Scholar
[7]Harrington, L., Understanding Lachlan s monster paper, 1980, typed notes.Google Scholar
[8]Lachlan, A. H., The impossibility of finding relative complements for recursively enumerable degrees, this Journal, vol. 31 (1966), pp. 434–454.Google Scholar
[9]Lachlan, A. H., Lower bounds for pairs of recursively enumerable degrees, Proceeding of the London Mathematical Society, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[10]Lachlan, A. H., Embedding nondistributive lattices in the recursively enumerable degrees, Conference in Mathematical Logic, London, 1970, Lecture Notes in Mathematics, vol. 255, Springer-Verlag, Berlin, Heidelberg, New York, 1972, pp. 149–177.Google Scholar
[11]Lachlan, A. H., A recursively enumerable degree which will not split over all lesser ones, Annals of Mathematical Logic, vol. 9 (1975), pp. 307–365.CrossRefGoogle Scholar
[12]Lachlan, A. H., Decomposition of recursively enumerable degrees, Proceeding of the American Mathematical Monthly, vol. 79 (1980), pp. 629–634.Google Scholar
[13]Lachlan, A. H. and Soare, R. I., Not every finite lattice is embeddable in the recursively enumerable degrees, Advances in Mathematics, vol. 37 (1980), pp. 74–82.CrossRefGoogle Scholar
[14]Sacks, G. E., On the degrees less than 0′, Annals of Mathematics, vol. 77 (1963), no. 2, pp. 211–231.CrossRefGoogle Scholar
[15]Sacks, G. E., The recursively enumerable degrees are dense, Annals of Mathematics, vol. 80 (1964), no. 2, pp. 300–312.CrossRefGoogle Scholar
[16]Shoenfield, J. R., Applications of model theory to degrees of unsolvability, Symposium on the theory of models, North-Holland, Amsterdam, 1965, pp. 359–363.Google Scholar
[17]Slaman, T. A., Notes on Lachlan's monster theorem, 1982, handwritten notes.Google Scholar
[18]Slaman, T. A., The density of infima in the recursively enumerable degrees, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 155–179.CrossRefGoogle Scholar
[19]Soare, R. I., Notes on Lachlan's monster theorem, 1983, handwritten notes.Google Scholar
[20]Soare, R. I., Recursively enumerable sets and degrees, Perspectives in mathematical logic, Omega Series, Springer-Verlag, Berlin, 1987.Google Scholar
[21]Thomason, S. K., Sublattices of the recursively enumerable degrees, Z. Math. Logik Grundlag. Math., vol. 17 (1971), pp. 273–280.CrossRefGoogle Scholar
[22]Yates, C. E. M., A minimal pair of recursively enumerable degrees, this Journal, vol. 31 (1966), pp. 159–168.Google Scholar