Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T07:18:09.039Z Has data issue: false hasContentIssue false
  • English
  • Français

The inclusion-exclusion principle for finitely many isolated sets

Published online by Cambridge University Press:  12 March 2014

J. C. E. Dekker
J. C. E. Dekker*
Affiliation:
Institute for Advanced Study, Princeton, New Jersey 08540 Department of Mathematics, Rutgers University, New Brunswick, New Jersey 08903
Get access Rights & Permissions [Opens in a new window]

Abstract

A nonnegative integer is called a number, a collection of numbers a set and a collection of sets a class. We write ε for the set of all numbers, o for the empty set, N(α) for the cardinality of α, ⊂ for inclusion and ⊂+ for proper inclusion. Let α, β 1,…, β k be subsets of some set υ. Then α′ stands for υ−α and β 1 … β k for β 1 ∩ … ∩ β k . For subsets α 1, …, α r of υ we write:

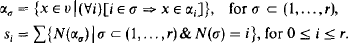
Note that α 0 = υ, hence s 0 = N(υ). If the set υ is finite, the classical inclusion-exclusion principle (abbreviated IEP) states

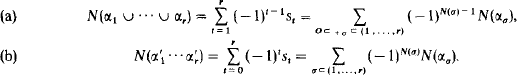
In this paper we generalize (a) and(b) to the case where α 1, …, α r are subsets of some countable but isolated set υ. Then the role of the cardinality N(α) of the set α is played by the RET (recursive equivalence type) Req α of α. These generalizations of (a) and (b) are proved in §3. Since they involve recursive distinctness, this notion is discussed in §2. In §4 we consider a natural extension of “the sum of the elements of a finite set σ” to the case where σ is countable. §5 deals with valuations, i.e., certain mappings μ from classes of isolated sets into the collection Λ of all isols which permit us to further generalize IEP by substituting μ(α) for Req α.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 2 , June 1986 , pp. 435 - 447
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barback, J., Regressive upper bounds, Rendiconti del Seminario Matematico della Università di Padova, voi. 39 (1967), pp. 248–272.Google Scholar
[2] Borges, R., On the principle of inclusion and exclusion, Periodica Mathematica Hungarica, vol. 3 (1973), pp. 149–156.CrossRefGoogle Scholar
[3] Cole, F. B., Personal communication.Google Scholar
[4] Comtet, L., Advanced combinatorics, Reidel, Boston, 1974.CrossRefGoogle Scholar
[5] Dekker, J. C. E., Regressive isols, Sets, models and recursion theory (Crossley, J. N., editor), North-Holland, Amsterdam, 1967, pp. 272–296.CrossRefGoogle Scholar
[6] Dekker, J. C. E., Isols and Burnside's lemma, Annals of Pure and Applied Logic (to appear).Google Scholar
[7] Dekker, J. C. E. and Myhill, J., Recursive equivalence types, University of California Publications in Mathematics (N.S.), vol. 3 ( 1960), pp. 67–214.Google Scholar
[8] Gersting, J. L., Infinite series of regressive isols under addition, Notre Dame Journal of Formal Logic, vol. 18 (1977), pp. 299–304.CrossRefGoogle Scholar
[9] Herstein, I. N. and Kaplansky, I., Matters mathematical, Chelsea, New York, 1974.Google Scholar
[10] McLaughlin, T. G. Regressive sets and the theory of isols, Marcel Dekker, New York, 1982.Google Scholar
[11] Liu, C. L., Elements of discrete mathematics, McGraw-Hill, New York, 1977.Google Scholar
[12] Nerode, A., Extensions to isols, Annals of Mathematics, ser. 2, vol. 73 (1961), pp. 362–403.CrossRefGoogle Scholar
[13] Nerode, A., Extensions to isolic integers, Annals of Mathematics, ser. 2, vol. 75 (1962), pp. 419–448.CrossRefGoogle Scholar
[14] Zeilberger, D., Garsia and Milne's bijective proof of the inclusion-exclusion principle, Discrete Mathematics, vol. 51 (1984), pp.109–110.CrossRefGoogle Scholar