Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-11T02:50:43.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Indifferent sets for genericity

Published online by Cambridge University Press:  12 March 2014

Adam R. Day
Adam R. Day*
Affiliation:
School of Mathematics, Statistics and Operations Research, Victoria University of Wellington, Wellington, New Zealand, E-mail: adam.day@math.berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates indifferent sets for comeager classes in Cantor space focusing of the class of all 1-generic sets and the class of all weakly 1-generic sets. Jockusch and Posner showed that there exist 1-generic sets that have indifferent sets [10]. Figueira, Miller and Nies have studied indifferent sets for randomness and other notions [7]. We show that any comeager class in Cantor space contains a comeager class with a universal indifferent set. A forcing construction is used to show that any 1-generic set, or weakly 1-generic set, has an indifferent set. Such an indifferent set can by computed by any set in 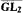which bounds the (weakly) 1-generic. We show by approximation arguments that some, but not all, 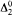1-generic sets can compute an indifferent set for themselves. We show that all 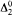weakly 1-generic sets can compute an indifferent set for themselves. Additional results on indifferent sets, including one of Miller, and two of Fitzgerald, are presented.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 1 , March 2013 , pp. 113 - 138
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barmpalias, George, Downey, Rod G., and Greenberg, Noam, Working with strong reducibilities above totally ω-c.e. and array computable degrees, Transactions of the American Mathematical Society, vol. 362 (2010), no. 2, pp. 777–813.CrossRefGoogle Scholar
[2]Cai, M. and Shore, R. A., Domination, forcing, array nonrecursiveness and relative recursive enumerability, this Journal, vol. 77 (2012), no. 1, pp. 33–48.Google Scholar
[3]Downey, R. G., Jockusch, Carl G. Jr., and Stob, Michael, Array nonrecursive sets and multiple permitting arguments, Recursion theory week (Oberwolfach, 1989), Lecture Notes in Mathematics, vol. 1432, Springer, Berlin, 1990, pp. 141–173.CrossRefGoogle Scholar
[4]Downey, Rod G. and Greenberg, Noam, A transfinite hierarchy of notions of lowness in the computably enumerable degrees, unifying classes, and natural definability, preprint.Google Scholar
[5]Downey, Rod G., Greenberg, Noam, and Weber, Rebecca, Totally ω-computably enumerable degrees and bounding critical triples, Journal of Mathematical Logic, vol. 7 (2007), no. 2, pp. 145–171.CrossRefGoogle Scholar
[6]Downey, Rod G., Jockusch, Carl G. Jr., and Stob, Michael, Array nonrecursive degrees and genericity, Computability, enumerability, unsolvability, London Mathematical Society Lecture Note Series, vol. 224, Cambridge University Press, Cambridge, 1996, pp. 93–104.CrossRefGoogle Scholar
[7]Figueira, Santiago, Miller, Joseph S., and Nies, André, Indifferent sets, Journal of Logic and Computation, vol. 19 (2009), no. 2, pp. 425–443.CrossRefGoogle Scholar
[8]Ishmukhametov, Shamil, Weak recursive degrees and a problem of Spector, Recursion theory and complexity (Kazan, 1997) (Arslanov, M. M. and Lempp, S., editors), de Gruyter Series in Logic and its Applications, vol. 2, de Gruyter, Berlin, 1999, pp. 81–88.CrossRefGoogle Scholar
[9]Jockusch, Carl G. Jr., Degrees of generic sets, Recursion theory: its generalisation and applications, London Mathematical Society Lecture Note Series, vol. 45, Cambridge University Press, Cambridge, 1980, pp. 110–139.CrossRefGoogle Scholar
[10]Jockusch, Carl G. Jr. and Posner, David B., Double jumps of minimal degrees, this Journal, vol. 43 (1978), no. 4, pp. 715–724.Google Scholar
[11]Kumabe, Masahiro, On the Turing degrees of generic sets, Ph.D. thesis, University of Chicago, 1990.Google Scholar
[12]Kumabe, Masahiro, Degrees of generic sets, Computability, enumerability, unsolvability, London Mathematical Society Lecture Note Series, vol. 224, Cambridge University Press, Cambridge, 1996, pp. 167–183.CrossRefGoogle Scholar
[13]Kurtz, S., Randomness and genericity in the degrees of unsolvability, Ph.D. thesis, University of Illinois at Urbana-Champaign, 1981.Google Scholar
[14]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar