Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T09:35:13.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite time Turing machines

Published online by Cambridge University Press:  12 March 2014

Joel David Hamkins  and
Andy Lewis
Joel David Hamkins
Affiliation:
Department of Mathematics, City University of New York, College of Staten Island, Staten Island, NY 10314., USA, E-mail: hamkins@postbox.csi.cuny.edu
Andy Lewis
Affiliation:
Department of Mathematics, Virginia Commonwealth University, Box #842014, Richmond, VA. 23284-2019, E-mail: amlewis@saturn.vcu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

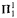We extend in a natural way the operation of Turing machines to infinite ordinal time, and investigate the resulting supertask theory of computability and decidability on the reals. Every set. for example, is decidable by such machines, and the semi-decidable sets form a portion of the 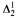sets. Our oracle concept leads to a notion of relative computability for sets of reals and a rich degree structure, stratified by two natural jump operators.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 2 , June 2000 , pp. 567 - 604
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bar]Barwise, John, Admissible Set Theory, Springer Verlag Publishing Company, New York, 1990.Google Scholar
[Dub]Dubose, Derrick Albert, The Equivalency of Determinacy and Iterated Sharps, this Journal, vol. 55 (1980), no. 2, pp. 502–510.Google Scholar
[Ear]Earman, John, Bangs, crunches, whimpers and shrieks: singularities and acausalities in relativistic spacetimes, The Clarendon Press, Oxford University Press, New York, 1995.CrossRefGoogle Scholar
[Ear & Nor]Earman, John and Norton, John D., Forever is a day: supertasks in Pitowski and Malament-Hogarth spacetimes, Philosophy of Science, vol. 60 (1993), no. 1, pp. 22–42.CrossRefGoogle Scholar
[Fef & Spc]Feferman, Solomon and Spector, C., Incompleteness along paths in progressions of theories, this Journal, vol. 27 (1962), pp. 383–390.Google Scholar
[Hog94]Hogarth, , Non-Turing computers and non-Turing computability, PSA 1994, Vol I East Lansing: Philosohpy of Science Association (Hull, D., Forbes, M., and Burian, R.B, editors), pp. 126–138.Google Scholar
[Hog92]Hogarth, , Does general relativity allow an observer to view an eternity in a finite time?, Foundations of Physics Letters, vol. 5 (1992), pp. 173–181.CrossRefGoogle Scholar
[Mos]Moschovakis, Yiannis Nicholas, Descriptive Set Theory, North-Holland Publishing Company, New York, 1980.Google Scholar
[Pit]Pitowsky, , The physical Church Thesis and Physical computational complexity, Iyyun, vol. 39 (1990), pp. 81–99.Google Scholar
[Sacks]Sacks, Gerald E., Higher Recursion Theory, Springer Verlag Publishing Company, New York, 1990.CrossRefGoogle Scholar
[Soare]Soare, Robert I., Recursively Enumerable Sets and Degrees, Springer Verlag Publishing Company, New York, 1987.CrossRefGoogle Scholar
[Thom]Thomson, , Tasks and Super-tasks, Analysis, vol. XV (1954–1955), pp. 1–13.CrossRefGoogle Scholar