Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T18:20:34.598Z Has data issue: false hasContentIssue false
  • English
  • Français

INTERPRETING ARITHMETIC IN THE FIRST-ORDER THEORY OF ADDITION AND COPRIMALITY OF POLYNOMIAL RINGS

Published online by Cambridge University Press:  09 May 2019

JAVIER UTRERAS
JAVIER UTRERAS*
Affiliation:
DEPARTAMENTO DE MATEMATICA FACULTAD DE CIENCIAS FISICAS Y MATEMATICAS UNIVERSIDAD DE CONCEPCION CONCEPCION, CHILEE-mail: javierutreras@udec.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the first-order theory of polynomial rings over a GCD domain and of the ring of formal entire functions over a non-Archimedean field in the language 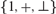$\{ 1, + , \bot \}$. We show that these structures interpret the first-order theory of the semi-ring of natural numbers. Moreover, this interpretation depends only on the characteristic of the original ring, and thus we obtain uniform undecidability results for these polynomial and entire functions rings of a fixed characteristic. This work enhances results of Raphael Robinson on essential undecidability of some polynomial or formal power series rings in languages that contain no symbols related to the polynomial or power series ring structure itself.

Keywords

Primary 03B25Secondary 12L05undecidabilitypolynomial ringslanguage of rings
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1194 - 1214
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, D. D., GCD domains, Gauss’ lemma and contents of polynomials, Non-Noetherian Commutative Ring Theory (Chapman, S. T. and Glaz, S., editors), Mathematics and its Application, vol 520. Springer, Boston, MA, 2000, pp. 1–31.Google Scholar
Bel’tjukov, A. P., Decidability of the universal theory of natural numbers with addition and divisibility. (Russian. English summary) Studies in constructive mathematics and mathematical logic, VII. Zap. Naucn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI), vol. 60 (1976), pp. 15–28, 221.Google Scholar
Bès, A., A survey of arithmetical definability, in: A tribute to Maurice Boffa. Société Mathématique de Belgique (2002), pp. 1–54.Google Scholar
Bosch, S., Güntzer, U., and Remmert, R., Non-Archimedean Analysis, Springer-Verlag, Berlin, 1984.Google Scholar
Denef, J., The Diophantine problem for polynomial rings and fields of rational functions. Transactions of the American Mathematical Society, vol. 242 (1978), pp. 391–399.Google Scholar
Denef, J., The Diophantine problem for polynomials rings of positive characteristic. Studies in Logic and the Foundations of Mathematics, vol. 97 (1979), pp. 131–145.Google Scholar
van den Dries, L. and Wilkie, A., The laws of integer divisibility, and solution sets of lineal divisibility conditions, this Journal, vol. 68 (2003), no. 2, pp. 503–526.Google Scholar
Garcia-Fritz, N. and Pasten, H., Uniform positive existential interpretation of the integers in rings of entire functions of positive characteristic. Journal of Number Theory, vol. 156 (2015), pp. 368–393.Google Scholar
Korec, I., Definability of addition from multiplication and neighborhood relation and some related results, preprint 23/1996 of Math. Institute SAV Bratislava.Google Scholar
Korec, I., A list of arithmetical structures complete with respect to the first–order definability. Theoretical Computer Science, vol. 257 (2001), no. 1, pp. 115–151.Google Scholar
Lipshitz, L., The Diophantine problem for addition and divisibility. Transactions of the American Mathematical Society, vol. 235 (1978), pp. 271–283.Google Scholar
Lipschitz, L. and Pheidas, T., An analogue of Hilbert’s tenth problem for p-adic entire functions, this Journal, vol. 60 (1995), no. 4, 1301–1309.Google Scholar
Naziazeno, E., Barone, M., and Caro, N., First-order definability of rational integers in a class of polynomial rings, 2017, arXiv:1703.08266.Google Scholar
Pheidas, T. and Zahidi, K., Undecidability of existential theories of rings and fields: A survey, in Hilbert’s tenth problem: Relations with arithmetic and algebraic geometry (Ghent, 1999). Contemporary Mathematics, vol. 270 (2000), pp. 49–106.Google Scholar
Pheidas, T. and Zahidi, K., Analogues of Hilbert’s tenth problem, Model Theory with Applications to Algebra and Analysis, vol. 2 (Chatzidakis, Z., Macpherson, D., Pillay, A., and Wilkie, A., editors), London Mathematical Society Lecture Note Series, vol. 350. Cambridge University Press, Cambridge, 2008, 207–236.Google Scholar
Richard, D., Answer to a problem raised by J. Robinson: The arithmetic of positive or negative integers is definable from successor and divisibility, this Journal, vol. 50 (1985), no. 4, pp. 927–935.Google Scholar
Richard, D., Definability in terms of the successor function and the coprimeness predicate in the set of arbitrary integers, this Journal, vol. 54 (1989), no. 4, pp. 1253–1287.Google Scholar
Riquelme, J.-L., Ultrametric value distribution in several variables and some consequences in logic, Ph.D. thesis, Universidad de Concepcion, Concepcion, Chile, 2015.Google Scholar
Robinson, J., Definability and decision problems in arithmetic, this Journal, vol. 14 (1949), no. 2, pp. 98–114.Google Scholar
Robinson, R., Undecidable rings. Transactions of the American Mathematical Society, vol. 70 (1951), pp. 137–159.Google Scholar
Vsemirnov, M., The Woods-Erdös conjecture for polynomial rings. Annals of Pure and Applied Logic, vol. 113 (2002), pp. 331–344.Google Scholar