Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chong, Chi Tat
and
Yu, Liang
2007.
Computation and Logic in the Real World.
Vol. 4497,
Issue. ,
p.
162.
Chong, C.
and
Yu, Liang
2009.
A Π¹₁-uniformization principle for reals.
Transactions of the American Mathematical Society,
Vol. 361,
Issue. 8,
p.
4233.
Wang, Wei
Wu, Liuzhen
and
Yu, Liang
2014.
Cofinal maximal chains in the Turing degrees.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 4,
p.
1391.
Hölzl, Rupert
Stephan, Frank
and
Yu, Liang
2016.
On Martin’s pointed tree theorem.
Computability,
Vol. 5,
Issue. 2,
p.
147.

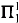 [
[