No CrossRef data available.
Article contents
A MINIMAL SET LOW FOR SPEED
Published online by Cambridge University Press: 03 January 2022
Abstract
An oracle A is low-for-speed if it is unable to speed up the computation of a set which is already computable: if a decidable language can be decided in time 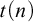 $t(n)$ using A as an oracle, then it can be decided without an oracle in time
$t(n)$ using A as an oracle, then it can be decided without an oracle in time 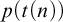 $p(t(n))$ for some polynomial p. The existence of a set which is low-for-speed was first shown by Bayer and Slaman who constructed a non-computable computably enumerable set which is low-for-speed. In this paper we answer a question previously raised by Bienvenu and Downey, who asked whether there is a minimal degree which is low-for-speed. The standard method of constructing a set of minimal degree via forcing is incompatible with making the set low-for-speed; but we are able to use an interesting new combination of forcing and full approximation to construct a set which is both of minimal degree and low-for-speed.
$p(t(n))$ for some polynomial p. The existence of a set which is low-for-speed was first shown by Bayer and Slaman who constructed a non-computable computably enumerable set which is low-for-speed. In this paper we answer a question previously raised by Bienvenu and Downey, who asked whether there is a minimal degree which is low-for-speed. The standard method of constructing a set of minimal degree via forcing is incompatible with making the set low-for-speed; but we are able to use an interesting new combination of forcing and full approximation to construct a set which is both of minimal degree and low-for-speed.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


