Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:30:18.253Z Has data issue: false hasContentIssue false
  • English
  • Français

Models for recursion theory

Published online by Cambridge University Press:  12 March 2014

Johan Moldestad  and
Dag Normann
Johan Moldestad
Affiliation:
Universitetet I Oslo, Oslo, Norway
Dag Normann
Affiliation:
Universitetet I Oslo, Oslo, Norway
Get access Rights & Permissions [Opens in a new window]

Extract

Several results in the theory of recursion in higher types indicate that the effect of a higher type functional on the lower types does not reflect the high type, i.e. the same effect could be obtained by functionals of relatively low type. The two main results here are:

Plus -1 - Theorem (G. Sacks [6] for k = 1, [7] for k > 1). Let H be a normal functional of type ≥ k + 1. Then there exists a normal functional F of type k + 1 such that k-sc(F) = k-sc(H), i.e. the same subsets of tp(k − 1) are recursive in F and H.

Plus - 2 - Theorem (L. Harrington [1]). Let H be a normal functional of type ≥ k + 2. Then there exists a normal functional F of type k +2 such that k-en(H) = k-en(F), i.e. the same subsets of tp(k − 1) are semirecursive in F and H.

The results in this paper also indicate that higher types cannot have too much influence on lower types. The key is the Skolem-Löwenheim theorem. Among the results we mention:

(1) Let n < m. A ⊆ tp(n) × tp(m) be Kleene-semicomputable. Let x ∈ B ⇔ ∀y∈tp(m), ⟨x, y⟩ ∈ A. Then B is 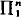. This result may be relativized to a functional of type n + 1.

(2) Let k0 be the type-k-functional that is constant zero. Let F be a functional of type < k. Then, for i ≤ k −2, i-sc(F ,k0) = i-sc(F), i-en(F, k0) = ∀tp(i)(i-en(F)).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 4 , December 1976 , pp. 719 - 729
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Harrington, L., Contributions to recursion theory on higher types, Ph. D. Thesis, M.I.T., 1973.Google Scholar
[2]Harrington, L. and MacQueen, D. B., Selection in abstract recursion theory, (to appear).Google Scholar
[3]Kleene, S. C., Recursive junctionals and quantifiers of finite types. I, Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52; and II, vol. 108 (1963), pp. 106–142.Google Scholar
[4]MacQueen, D. B., Post's problem for recursion in higher types, Ph. D. Thesis, M.I.T., 1972.Google Scholar
[5]Moldestad, J. and Normann, D., 2-envelopes And the analytic hierarchy, preprint series, Oslo, No. 21, 1974.Google Scholar
[6]Sacks, G. E., The 1-section of a type n object, Generalized recursion theory (edited by Fenstad, J. E. and Hinman, P.), pp. 81–93, North-Holland, Amsterdam, 1974.Google Scholar
[7]Sacks, G. E., The k-section of a type n object, American Journal of Mathematics (to appear).Google Scholar
[8]Moschovakis, Y. N., Structural characterizations of classes of relations, Generalized recursion theory (edited by Fenstad, and Hinman, ), pp. 53–80, North-Holland, Amsterdam, 1974.Google Scholar
[9]Bergstra, J., unpublished notes, Utrecht, 1974.Google Scholar
[10]Moschovakis, Y. N., Hyperanalytic predicates, Transactions of the American Mathematical Society, vol. 129 (1967), pp. 249–282.CrossRefGoogle Scholar
[11]Cenzer, D., Inductively defined sets of reals, Bulletin of the American Mathematical Society, vol. 80 (1974), pp. 485–487.CrossRefGoogle Scholar
[12]Moschovakis, Y. N., Elementary induction on abstract structures, North-Holland, Amsterdam, 1974.Google Scholar